First, please create an account

Already have a Sophia account?

Absolute Value Equations

Author: Sophia

what's covered

In this lesson, you will learn how to solve an absolute value equation. Specifically, this lesson will cover:

1. Absolute Value Review
2. Equations in the Form |x |
3. Equations in the Form |mx + b |

1. Absolute Value Review

The absolute value of a number is the distance from zero on the number line. Distance is never a negative value, so absolute value never returns a negative.

We can look at the number line and see that the absolute value of a positive number and the absolute value of a negative number are both positive:

Both -4 and 4 are 4 units away from zero on the number line. We can say that open vertical bar 4 close vertical bar equals 4 and open vertical bar negative 4 close vertical bar equals 4 .

This leads to a piecewise definition of absolute value:

formula to know

Absolute Value

open vertical bar x close vertical bar equals open curly brackets table attributes columnalign left end attributes row cell x comma space when space x greater or equal than 0 end cell row cell negative x comma space when space x less than 0 end cell end table close

This means that if x is zero or greater, the value of x does not change when we apply the absolute value. However, if x is negative, we change the sign of x when applying the absolute value, so as to make it positive.

2. Equations in the Form |x |

When we solve any absolute value equation, we just remember that the expression can be positive or negative, and still have the same absolute value. For this reason, we create two separate equations: one with a positive value, and one with a negative value, for the expression inside absolute value bars:


	Create two equations
	Our solution

To solve absolute value equations, we can remove the absolute value bars only if we create two equations: one equation will look nearly identical to the original absolute value equation, while the second equation will consider the case when the expression is negative.

Next, we will consider more complex absolute value equations

3. Equations in the Form |mx + b |

Once again, we are going to solve this equation by creating two separate equations without absolute value bars. One equation will contain the expression exactly as it appears within the absolute value bars. The second equation must consider the case when the expression has the opposite value. That is, we reverse the sign on the other side of the equation:

EXAMPLE

Find the solutions to the absolute equation 14 equals open vertical bar 3 x plus 2 close vertical bar

	Create two equations
	Solve each equation

Next, we solve each equation individually and include both solutions for x as solutions to the absolute value equation.

	Solve the first equation by subtracting 2 from both sides
	Divide both sides by 3
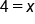
	Our solution

	Solve the second equation by subtracting 2 from both sides
	Divide both sides by 3
$fraction numerator short dash 16 over denominator 3 end fraction equals x$	Convert into a decimal
	Our solution

The solutions to 14 equals open vertical bar 3 x plus 2 close vertical bar

are

x equals short dash 5.33 with bar on top comma space 4

big idea

Create two equations, each without absolute value bars. One equation will remain the same in every other respect, while the second equation will have the opposite value (reversed sign) on the other side of the equation.

summary

The absolute value of a number is its distance from 0 on the number line, and is always non-negative. We discussed two types of absolute value equations: equations in the form lx l and equations in the form lmx + b l. When solving absolute value equations, we must consider both the positive and negative values of the expression inside the absolute value bars, because they can equal the same value once we take the absolute value. Also, when solving absolute value equations, the first step is to isolate the absolute value expression on one side of the equation.

Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License

Formulas to Know

Absolute Value: $open vertical bar x close vertical bar equals open curly brackets table attributes columnalign left end attributes row cell x comma space when space x greater or equal than 0 end cell row cell negative x comma space when space x less than 0 end cell end table close$

First, please create an account

Absolute Value Equations

Table of Contents

1. Absolute Value Review

2. Equations in the Form |x |

3. Equations in the Form |mx + b |