Table of Contents |
When an inequality has an absolute value we will have to remove the absolute value in order to graph the solution or give interval notation. The way we remove the absolute value depends on the direction of the inequality symbol. Recall that absolute value is defined as the distance from zero.
EXAMPLE
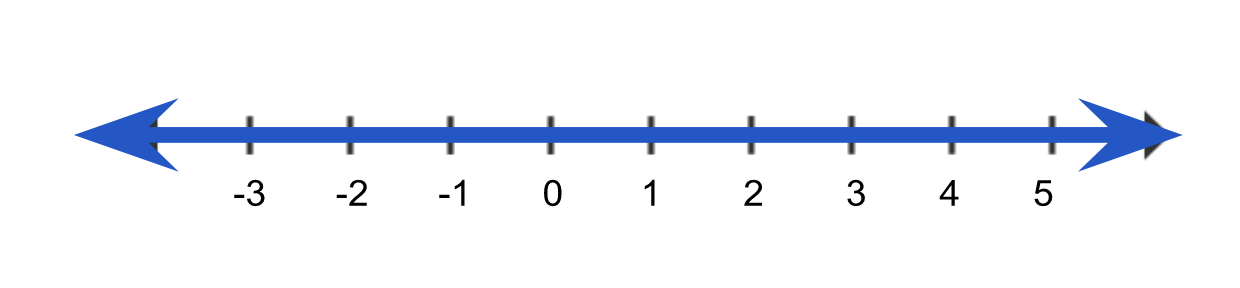
Consider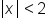 .
.
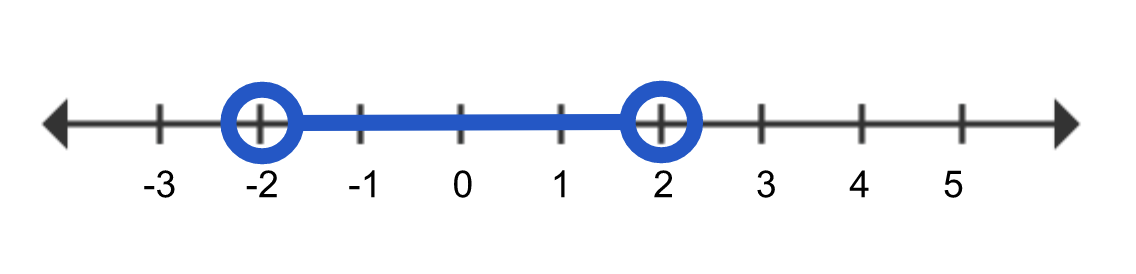
This graph looks just like the graphs of the three-part compound inequalities! When the absolute value is less than a number we will remove the absolute value by changing the problem to a three-part inequality, with the negative value on the left and the positive value on the right. So in the example above, 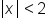 becomes
becomes 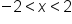 , as the graph above illustrates, and can be expressed with the following formula:
, as the graph above illustrates, and can be expressed with the following formula:
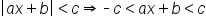
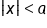
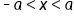
 is a type of "AND" compound inequality.
is a type of "AND" compound inequality.
Let's look at a case when the absolute value inequality is "greater than".
EXAMPLE
Consider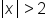 .
.
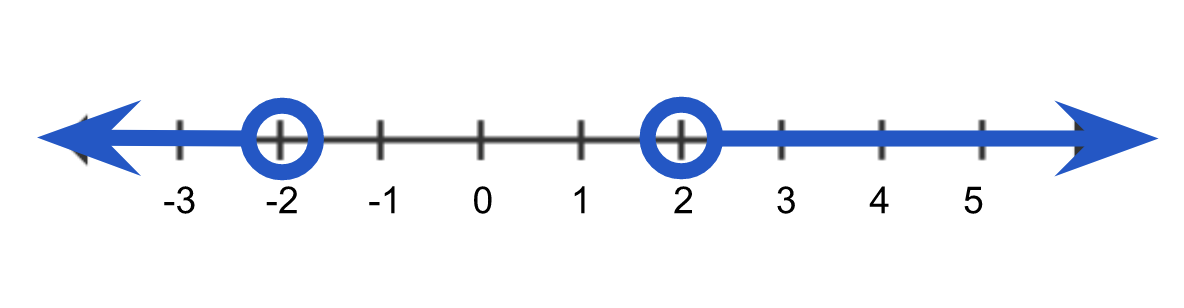
This graph looks just like the graphs of the OR compound inequalities! When the absolute value is greater than a number we will remove the absolute value by changing the problem to an OR inequality, the first inequality looking just like the problem with no absolute value, the second flipping the inequality symbol and changing the value to a negative. So 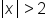 becomes
becomes 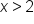 or
or  , as the graph above illustrates, and can be expressed with the following formula:
, as the graph above illustrates, and can be expressed with the following formula:

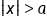
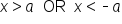
 is a type of "OR" compound inequality.
is a type of "OR" compound inequality.
| Absolute Inequality | Rewrite as.... |
|---|---|
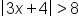
|
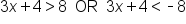
|

|

|
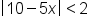
|

|
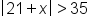
|
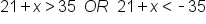
|
We can solve absolute value inequalities much like we solved absolute value equations by following these steps.
EXAMPLE
Solve the inequality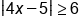 , graph the solution, and give interval notation of the solution.
, graph the solution, and give interval notation of the solution.
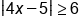
|
Absolute value is greater than, use OR |
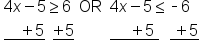
|
Solve by adding 5 to both sides in both inequalities |
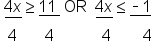
|
Divide both sides by 4 in both inequalities |

|
Our Solution |
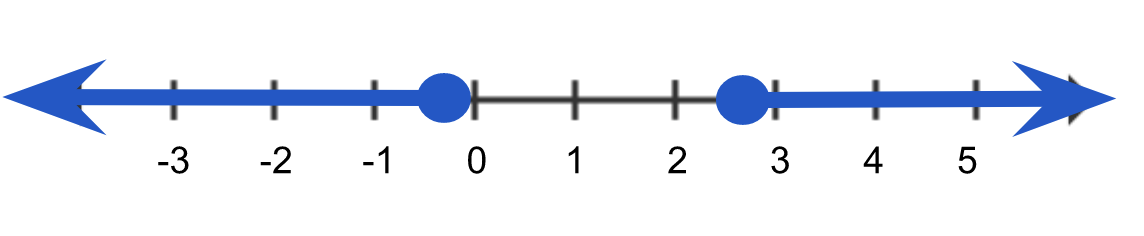
![open parentheses short dash infinity comma short dash 1 fourth text ] end text union left square bracket 11 over 4 comma infinity close parentheses](https://sophialearning.s3.amazonaws.com/wiris_cache/4201/formula.png)
EXAMPLE
Solve the inequality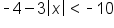 , graph the solution, and give interval notation of the solution.
, graph the solution, and give interval notation of the solution.
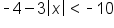 
|
First add 4 to both sides to isolate the absolute value |
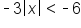 
|
Divide both sides by  . Dividing by a negative switches the symbol! . Dividing by a negative switches the symbol!
|
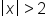
|
Absolute value is greater than, use OR; |
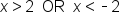
|
Our Solution |
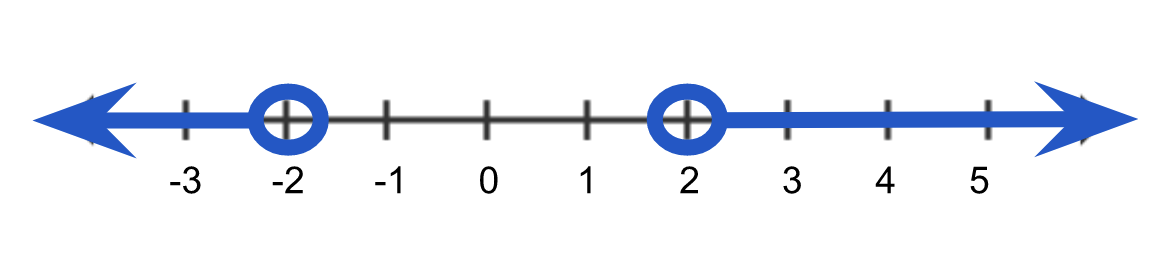
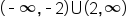
EXAMPLE
Solve the inequality , graph the solution, and give interval notation of the solution.
, graph the solution, and give interval notation of the solution.
 
|
Subtract 9 from both sides |
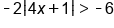 
|
Divide both sides by  . Dividing by negative switches the symbol! . Dividing by negative switches the symbol!
|
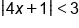
|
Absolute value is less than, use three part inequality |
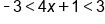 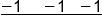
|
Subtract 1 from all three parts |
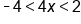 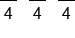
|
Divide all three parts by 4 |
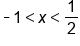
|
Our solution |
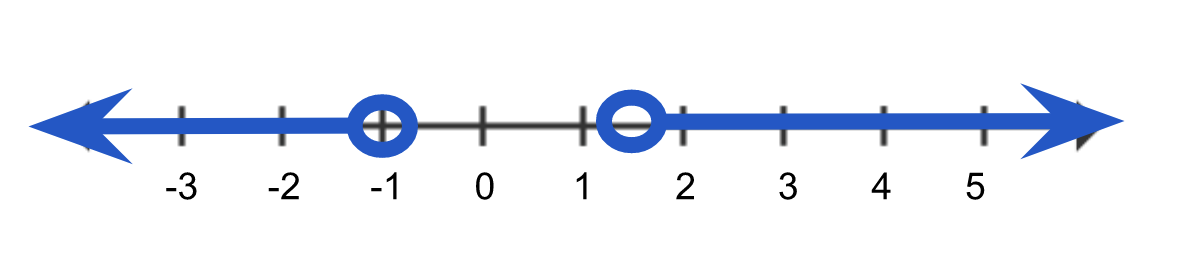
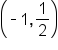
It is important to remember as we are solving these equations, the absolute value is always positive. There are cases where there is no solution to the inequality or all real numbers are the solution:
EXAMPLE
Solve the inequality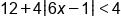 , graph the solution, and give interval notation of the solution.
, graph the solution, and give interval notation of the solution.
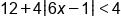 
|
Subtract 12 from both sides |
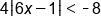 
|
Divide both sides by 4 |
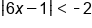
|
Absolute value can't be less than a negative, NO SOLUTION |

EXAMPLE
Solve the inequality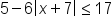 , graph the solution, and give interval notation of the solution.
, graph the solution, and give interval notation of the solution.
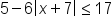 
|
Subtract 5 from both sides |
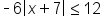 
|
Divide both sides by  . Dividing by a negative flips the symbol! . Dividing by a negative flips the symbol!
|

|
Absolute value is always greater than negative, ALL REAL NUMBERS |
Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License