Adding and Subtracting Radical Expressions

1. Adding and Subtracting Radical Expressions

Adding and subtracting radicals is very similar to adding and subtracting with variables. Consider the following example:

EXAMPLE

Evaluate the following expression that has variables:

	Combine like terms
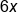
	Our Solution

EXAMPLE

Evaluate the following expression that has radicals:

	Combine like terms
	Our Solution

Notice that when we combined the terms with it was just like combining terms with x. When adding and subtracting with radicals we can combine like radicals just as like terms. We add and subtract the coefficients in front of the radical, and the radical stays the same.

EXAMPLE

	Combine like radicals and
	Our Solution

We cannot simplify this expression anymore as the radicals do not match. Often problems we solved have no like radicals, however, if we first simplify the radicals, we may find we do in fact have like radicals.

EXAMPLE

	Simplify radicals, find perfect square factors.
	Take roots where possible
	Combine like terms
	Our Solution

2. Adding and Subtracting With Higher Indices

This exact process can be used to add and subtract radicals with higher indices. Indices is the plural of index, which indicates the type of root.

EXAMPLE

	Simplify each radical, finding perfect cube factors.
	Take roots where possible
	Multiply coefficients
	Combine like terms
	Our Solution