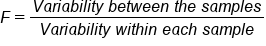This tutorial will cover tests for three or more population means and the process for analysis of variance (ANOVA). Our discussion breaks down as follows:
1. ANOVA
Comparing three or more means requires a new hypothesis test called analysis of variance (ANOVA). The AN is for "analysis", the O is for "of", and the VA is for "variance"). For ANOVA, we compare the means by analyzing the sample variances from the independently selected sample.
-
EXAMPLE
Suppose a factory supervisor wants to know whether it takes his workers different amounts of time to complete a task based on their proficiency level. The factory employs apprentices, novices, and masters. The supervisor randomly selects ten workers from each group and has them perform the task.
The summary of the data, which is the time in minutes to complete the task, is shown in this table here:
|
Proficiency
|
n
|
x̄
|
s
|
|
Apprentice
|
10
|
22.5
|
4.2
|
|
Novice
|
10
|
20.7
|
5.1
|
|
Master
|
10
|
19.0
|
4.6
|
Are these sample means significantly different from each other? In order to answer this question, you will need to perform the analysis of variance (ANOVA) because we are comparing three population means.
-
- Analysis of Variance (ANOVA)
- A hypothesis test that allows us to compare three or more population means.
1a. Conditions
There are a few conditions necessary for an ANOVA test:
- Independent samples from the populations.
- Each population has to be normally distributed.
- The variances, and therefore the standard deviations of all those normal distributions, are the same.
For the above factory scenario, let's assume that the above three conditions are met.
1b. Null and Alternative Hypothesis
Once the three conditions are met, we can identify the null and alternative hypotheses and choose an alpha level.
For our factory scenario:
Null
Hypothesis
|
H0: μA = μN = μM; The mean time required to complete the task is the same for the masters, the novices, and the apprentices.
|
Alternative
Hypothesis
|
Ha: At least one of the mean times is different from another.
|
Alpha
Level
|
α = 0.05
|
1c. F-Statistic
When you do an ANOVA test, the statistic that you use is not going to be a z or t, as you have been using in the past. Instead, you will use what is called an "F". An F statistic is calculated by taking the quotient of the variability between the samples and the variability within each sample.
-
- F-Statistic
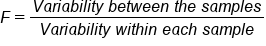
The size of F can provide information about the null hypothesis:
- Small F Statistic: Consistent with the null hypothesis, meaning H0 is true.
- Large F Statistic: Evidence against the null hypothesis, meaning there's more variability between the samples than there are within the samples. This would be rare if the null hypothesis was true.
-
A small F is consistent with the null hypothesis, versus a large F statistic, which is evidence against the null hypothesis. You wouldn't reject it if F was small.
Almost always, you will calculate the ANOVA F statistic and the p-value with technology. All but the most simple, straightforward problems will be calculated using technology.
In our factory scenario, the F statistic, calculated with technology, is 1.418. That is not a very large value of F. The corresponding p-value is 0.26, which is a very large p-value.
-
- F Statistic
- The test statistic in an ANOVA test. It is the ratio of the variability between the samples to the variability within each sample. If the null hypothesis is true, the F statistic will probably be small.
1d. Concluding the ANOVA Test
Finally, we need to decide whether to reject or fail to reject the null hypothesis.
- If the p-value is less than the significance level, you would reject the null hypothesis.
- If the p-value is greater than the significance level, you would fail to reject the null hypothesis.
In the factory scenario, since the p-value of 0.26 is very large, greater than the 0.05 significance level, you fail to reject the null hypothesis. There's no evidence that suggests that the time required to complete the task differs significantly with proficiency level.
ANOVA, or analysis of variance, allows you to compare three or more means by comparing the variability within each sample to the variability between the samples. The null hypothesis is that all the means are the same, and the alternative hypothesis is that at least one of them is different. A small F is consistent with the null hypothesis, versus a large F statistic, which is evidence against the null hypothesis. The F and the p-value are almost always calculated with technology.
Good luck!