EXAMPLE
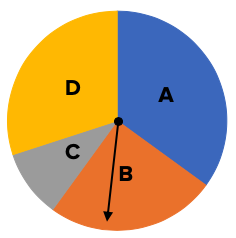
Suppose a coin is flipped and this spinner is spun, where A and D are a lot more common than B or C
Since the outcome of the coin flip doesn't have any influence on the probabilities for the spinner, these events are called independent. Spinning the spinner wouldn't have any effect on the probability of the coin coming up heads, and knowing if the coin came up heads doesn't affect the probabilities for the spinner.
You can create a tree diagram to show all the possible outcomes:

There are two outcomes for the quarter, and there are four outcomes for the spinner. Using the Fundamental Counting Principle, we know that there are 2 times 4, or 8 total outcomes. However, they're not all equally likely.
The heads and tails each have a one-half probability, but A, B, C, and D don't all have the same probability. If you look closely at the spinner, A is the biggest sector with 35%, followed by D with 30%, then B with 25% and C with 10%.

Since it doesn't matter whether you got heads the first time or tails the first time--the probabilities will remain the same--you can apply the ratios down below too.

Suppose that you did this experiment 1,000 times. You would expect about 500 heads and 500 tails if everything went according to your expectation.
If the second group went according to your expectation, 35% of those 500 would say A, 25% of those 500 would say B, 10% of those 500 would say C, and 30% of those 500 would say D.
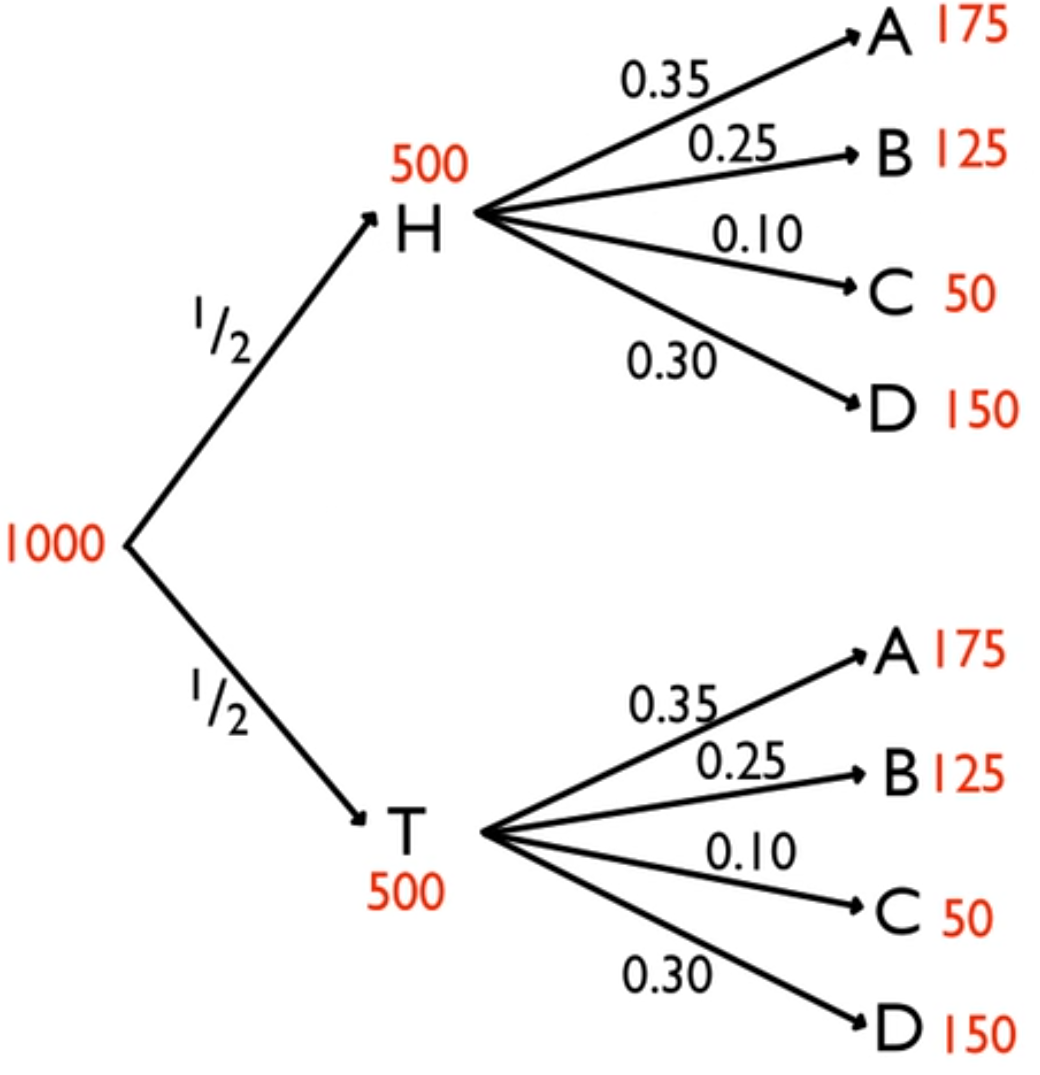
Ultimately, you would end up with 175 of the 1,000 that went flipped heads and landed on A, 125 of the 1,000 that went flipped heads and landed on B, etc.
But what if you wanted to know the probability of flipping heads and landing on D? This would be 150 of the 1,000, and when simplified, equals 0.15.
Is there another way to obtain 0.15?
Look at the path that you traveled to get here. You went from heads down to D. You had those probabilities of 0.5 and 0.3, and the probability of H and D was 0.15. Hopefully, what you're seeing is that these two values multiplied equals 0.15.
In this case, it was 1/2 for heads and 0.3 for D. Multiply them, and you get 0.15.