Take a look back at what congruent segments are.
What is a ray?
What is an angle?
Just like line segments, angles can be congruent.
Two angles are congruent when they have the same measure.
Example:
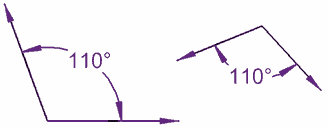
We can show that two angles are congruent by using a little "tick" like we do with congruent line segments.
To see an example, look at angles  and angles
and angles 

If a ray divides a larger angle into two smaller, congruent angles, it is called an angle bisector.
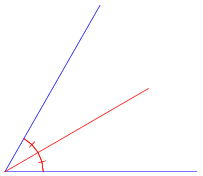
When two lines intersect, they form some angles. These are some of the relationships between those angles.
Two angles that sum up to  are called complementary angles.
are called complementary angles.
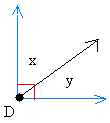
(Angles x and y are complementary angles)
Two angles that sum up to  are called supplementary angles.
are called supplementary angles.
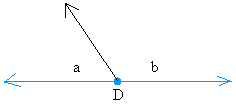
(Angles a and b are supplementary angles)