Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Applying Properties of Logarithms

Author: Sophia
PDF Version

what's covered
In this lesson, you will learn how to evaluate a logarithmic expression using the properties of logarithms. Specifically, this lesson will cover:

Table of Contents

1. Applying the Log-Exponent Relationship

Keeping the log-exponent relationship in mind can help us rewrite logarithmic expressions and evaluate them. Exponents and logarithms are inverse operations, and we can rewrite these two kinds of expressions in the following way:

  • Exponential expression: y equals b to the power of x
  • Logarithmic expression: log subscript b open parentheses y close parentheses equals x
We can connect these two expressions in the following way:

formula to know
Logarithmic Form to Exponential Form
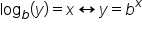
log subscript b open parentheses y close parentheses equals x left right arrow y equals b to the power of x

EXAMPLE

Evaluate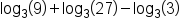 log subscript 3 left parenthesis 9 right parenthesis plus log subscript 3 left parenthesis 27 right parenthesis minus log subscript 3 left parenthesis 3 right parenthesis.

We can apply various properties of logs to simplify and evaluate this expression. First, let's use the inverse relationship between exponents and logs to think about how to evaluate each logarithmic term individually:

log subscript 3 open parentheses 9 close parentheses equals x Rewrite as an exponential expression
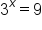
3 to the power of x equals 9 x equals 2 makes this true
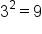
3 squared equals 9 Use the Log-Exponent Relationship
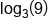
log subscript 3 open parentheses 9 close parentheses equals 2 Our solution for log subscript 3 open parentheses 9 close parentheses

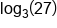
log subscript 3 open parentheses 27 close parentheses Rewrite as an exponential expression
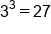3 to the power of x equals 27 3 cubed equals 27 makes this true
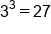
3 cubed equals 27 Use the Log-Exponent Relationship
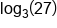
log subscript 3 open parentheses 27 close parentheses equals 3 Our solution for log subscript 3 open parentheses 27 close parentheses

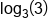
log subscript 3 open parentheses 3 close parentheses Rewrite as an exponential expression
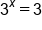
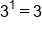3 to the power of x equals 3 3 to the power of 1 equals 3 makes this true
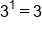
3 to the power of 1 equals 3 Use the Log-Exponent Relationship
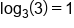
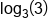
log subscript 3 open parentheses 3 close parentheses equals 1 Our solution for log subscript 3 open parentheses 3 close parentheses

We can now rewrite our original expression as:

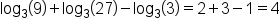
log subscript 3 open parentheses 9 close parentheses plus log subscript 3 open parentheses 27 close parentheses minus log subscript 3 open parentheses 3 close parentheses equals 2 plus 3 minus 1 equals 4

2. Applying the Product and Quotient Properties

Let's simplify and evaluate the same expression, but this time we will use the product property of logs and quotient properties of logs.

formula to know
Product Property of Logs
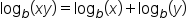
log subscript b left parenthesis x y right parenthesis equals log subscript b left parenthesis x right parenthesis plus log subscript b left parenthesis y right parenthesis
Quotient Property of Logs
log subscript b left parenthesis x over y right parenthesis equals log subscript b left parenthesis x right parenthesis minus log subscript b left parenthesis y right parenthesis

In our first example, we have some logarithms with the same base being added and subtracted. When we see addition, we can combine them into one logarithm by multiplying the arguments. Similarly, when we see subtraction, we can combine them into one logarithm using division.

EXAMPLE

Evaluate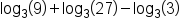 log subscript 3 left parenthesis 9 right parenthesis plus log subscript 3 left parenthesis 27 right parenthesis minus log subscript 3 left parenthesis 3 right parenthesis using the Product Property and Quotient Property of Logs.

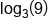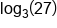
log subscript 3 open parentheses 9 close parentheses plus log subscript 3 open parentheses 27 close parentheses minus log subscript 3 open parentheses 3 close parentheses Use the Product Property of Logs to combine log subscript 3 open parentheses 9 close parentheses and log subscript 3 open parentheses 27 close parentheses
log subscript 3 open parentheses 9 times 27 close parentheses minus log subscript 3 open parentheses 3 close parentheses Evaluate multiplication in parentheses
log subscript 3 open parentheses 243 close parentheses minus log subscript 3 open parentheses 3 close parentheses Use the Quotient Property of Logs to combine 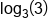log subscript 3 open parentheses 243 close parentheses and log subscript 3 open parentheses 3 close parentheses
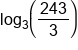
log subscript 3 open parentheses 243 over 3 close parentheses Evaluate division in parentheses
log subscript 3 open parentheses 81 close parentheses Rewrite as an exponential expression
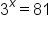
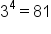3 to the power of x equals 81 3 to the power of 4 equals 81 makes this true
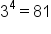
3 to the power of 4 equals 81 Use the Log-Exponent Relationship
4 Our solution

3. Applying Multiple Properties

Recall other properties of logarithms:

formula to know
Change of Base Property of Logs
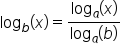
log subscript b open parentheses x close parentheses equals fraction numerator log subscript a open parentheses x close parentheses over denominator log subscript a open parentheses b close parentheses end fraction
Power Property of Logs
log subscript b open parentheses x to the power of n close parentheses equals n times log subscript b open parentheses x close parentheses
Other Properties of Logs
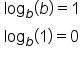
table attributes columnalign left end attributes row cell log subscript b open parentheses b close parentheses equals 1 end cell row cell log subscript b open parentheses 1 close parentheses equals 0 end cell end table

Consider which of the above properties, along with the other properties in this lesson, you would need to simplify and evaluate the following logarithmic expression:

EXAMPLE

Simplify and evaluate the logarithmic expression log subscript a open parentheses fraction numerator x z over denominator y squared end fraction close parentheses when given the following:

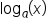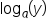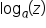table attributes columnalign left end attributes row cell log subscript a open parentheses x close parentheses equals 3 end cell row cell log subscript a open parentheses y close parentheses equals 5 end cell row cell log subscript a open parentheses z close parentheses equals short dash 2 end cell end table

Inside the logarithm, we see multiplication, division, and an exponent. This tells us that we will likely use the Product, Quotient, and Power Properties. We are also given the values of log subscript a open parentheses x close parentheses, log subscript a open parentheses y close parentheses, and log subscript a open parentheses z close parentheses, which will come in handy later in our evaluation.

log subscript a open parentheses fraction numerator x z over denominator y squared end fraction close parentheses Apply the Product and Quotient Properties of Logs
log subscript a open parentheses x close parentheses plus log subscript a open parentheses z close parentheses minus log subscript a open parentheses y squared close parentheses Apply the Power Property of Logs
log subscript a open parentheses x close parentheses plus log subscript a open parentheses z close parentheses minus 2 log subscript a open parentheses y close parentheses Substitute the values 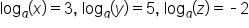log subscript a open parentheses x close parentheses equals 3 comma space log subscript a open parentheses y close parentheses equals 5 comma space log subscript a open parentheses z close parentheses equals short dash 2
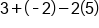
3 plus open parentheses short dash 2 close parentheses minus 2 open parentheses 5 close parentheses Evaluate multiplication
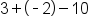
3 plus open parentheses short dash 2 close parentheses minus 10 Simplify
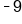
short dash 9 Our solution

EXAMPLE

Evaluate the logarithmic expression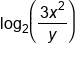 log subscript 2 open parentheses fraction numerator 3 x squared over denominator y end fraction close parentheses when given the following:

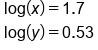
table attributes columnalign left end attributes row cell log open parentheses x close parentheses equals 1.7 end cell row cell log open parentheses y close parentheses equals 0.53 end cell end table

Just like the above example, we see multiplication, division, and an exponent so we will again use the Product, Quotient, and Power Properties. However, notice the difference in bases. The expression we need to evaluate has a log of base 2, whereas the log values we are given are common logs, which have a base of 10. This means we'll need to use the Change of Base Property as well.

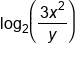
log subscript 2 open parentheses fraction numerator 3 x squared over denominator y end fraction close parentheses Apply the Product and Quotient Properties of Logs
log subscript 2 open parentheses 3 close parentheses plus log subscript 2 open parentheses x squared close parentheses minus log subscript 2 open parentheses y close parentheses Apply the Power Property of Logs
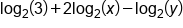
log subscript 2 open parentheses 3 close parentheses plus 2 log subscript 2 open parentheses x close parentheses minus log subscript 2 open parentheses y close parentheses Apply the Change of Base Property
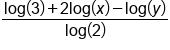
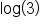
fraction numerator log open parentheses 3 close parentheses plus 2 log open parentheses x close parentheses minus log open parentheses y close parentheses over denominator log open parentheses 2 close parentheses end fraction Substitute the values log open parentheses x close parentheses equals 1.7 comma space log open parentheses y close parentheses equals 0.53 and use calculator to evaluate log open parentheses 3 close parentheses
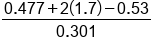
fraction numerator 0.477 plus 2 open parentheses 1.7 close parentheses minus 0.53 over denominator 0.301 end fraction Simplify numerator
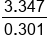
fraction numerator 3.347 over denominator 0.301 end fraction Divide
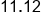
11.12 Our solution, rounded to the nearest hundredth

summary
When applying the log-exponent relationship, recall that a logarithmic equation can be written as an exponential equation. When applying the product and quotient properties, remember that the product property says that log base b of some product x and y is equal to log base b of x plus log base b of y. The quotient property says that log base b of some quotient x and y is equal to log base b of x minus log base b of y. The power property says that log base b of x to the nth power is equal to n times log base b of x. When evaluating a logarithmic expression, you may apply multiple properties.

Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License

Formulas to Know
Change of Base Property of Logs

log subscript b left parenthesis x right parenthesis equals fraction numerator log subscript a left parenthesis x right parenthesis over denominator log subscript a left parenthesis b right parenthesis end fraction

Logarithmic Form to Exponential Form

log subscript b open parentheses y close parentheses equals x space left right arrow y equals b to the power of x

Other Properties of Logs

log subscript b left parenthesis b right parenthesis equals 1

log subscript b left parenthesis 1 right parenthesis equals 0

Power Property of Logs

log subscript b open parentheses x to the power of n close parentheses equals n times log subscript b left parenthesis x right parenthesis

Product Property of Logs

log subscript b left parenthesis x y right parenthesis equals log subscript b left parenthesis x right parenthesis plus log subscript b left parenthesis y right parenthesis

Quotient Property of Logs

log subscript b open parentheses x over y close parentheses equals log subscript b left parenthesis x right parenthesis minus log subscript b left parenthesis y right parenthesis

© 2024 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.