Basic Quadratic Factoring

1. FOIL: A Review

In review, FOIL is an acronym used to remember the steps for multiplying terms in binomial multiplication. It stands for:

First
Outside
Inside
Last

EXAMPLE

If you are multiplying the two binomials shown below, you start by multiplying your first two terms in each parentheses, followed by your outside terms, then your inside terms, and finally, your last terms.



In the resulting expression, combine your two like terms to arrive at your final answer.

This resulting expression is a quadratic expression that can be generally written in this form:

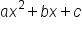
Quadratic expressions in this form have an x-squared term, an x term, and a constant term. Quadratic factoring is the reverse process of FOILing. Therefore, you could factor your resulting expression above, and the result would be your original expression, multiplying the two binomials.

2. Factoring Quadratics

Factoring quadratic expressions is useful when solving quadratic equations, and provides important information about the graphs of quadratic equations.

EXAMPLE

Consider the previous example to look at the process for factoring quadratics. You can see that the constant term 15 in expanded form is the product of the two numbers in factored form, 3 and 5.

Expanded Form:
Factored Form:

You can also see that the coefficient of the x term in expanded form, 8, is the sum of the two numbers in factored form.

Expanded Form:
Factored Form:

When you factor a quadratic expression in expanded form, you use these two patterns to identify the two numbers to use in the factored form of the expression.

step by step

1. Identify the pairs of numbers that, when multiplied together, equal the constant term.
2. Add your factor pairs to find the pair of numbers that, when added together, also equal the coefficient of your x term.
3. Use this pair of numbers to write the expression in factored form.

2a. Positive x-Term, Positive Constant Term

Using the same expanded form expression from above, how would you write it into factored form?

Step 1: Identify the pairs of numbers that, when multiplied together, equal the constant term, which in this case is 15 ():

hint

When considering factor pairs for a constant term, both positive and negative numbers should be considered. This will be especially important when there is a subtraction in the expanded form, as this indicates that at least one number in the factor pair will be negative.

The factor pairs of 15 are as follows:

Step 2: Add your factor pairs to find the pair of numbers that, when added together, also equal the coefficient of your x term, in this case, 8 ():

Factors of 15	Add to 8
1, 15 ✘
-1, -15 ✘
3, 5 ✔
-3, -5

Once you have found the pair of numbers with the correct sum, you do not need to consider other factor pairs, because there will be only one pair of numbers that will multiply to the constant term and add to the x term coefficient. In this example, 3 and 5 are your pair of numbers that multiply to 15 and add to 8.

Step 3: Use this pair of numbers to write the expression in factored form.

Therefore, .

2b. Positive x-Term, Negative Constant Term

Suppose you want to factor the expression:

Start by identifying the pair of numbers that, when multiplied together, equal -12 (). Now, because your constant term is negative, you know that one of the numbers must be negative and the other one will be positive. The pairs of numbers that multiply to -12 are:

Next, look for which pair also has a sum of 4 ():

Factors of 12	Add to 4
-1, 12 ✘
1, -12 ✘
-2, 6 ✔
2, -6
-3, 4
3, -4

Now you can use your two numbers, -2 and 6, to write your expression in factored form.

You can verify that you correctly factored the expression by multiplying the binomials together using FOIL to ensure that you arrive back at your original expression.

This is the same as your original expression, which means your answer is the correct factored form.

Therefore, .

2c. Negative x-Term, Positive Constant Term

Suppose you want to factor the expression:

Start by identifying the pairs of numbers that, when multiplied together, equal 10 (). Note that because the pair of numbers must multiply to a positive number but add to a negative number, both of the numbers must be negative.

Now, look for which of these pairs of numbers also have a sum of -7.

Factors of 10	Add to -7
-1, -12 ✘
-2, -5 ✔

Therefore, you use the pair (-2, -5) to write your expression in factored form.

Therefore, .

2d. Negative x-Term, Negative Constant Term

Use what you’ve learned so far about quadratic factoring to factor this last expression:

Can you identify the pairs of numbers that, when multiplied together, equal -2? Remember, because the pair of numbers must multiply to a negative number and add to a negative number, one of the numbers will be positive and one will be negative.

Now, because there’s no written number in front of the x term, the x term has an implied coefficient of -1. Therefore, look for which of these number pairs also has the sum of -1.

Factors of -2	Add to -1
-1, 2 ✘
1, -2 ✔

Since you’ve determined that 1 and -2 add to a -1, you can use this pair of numbers to write your expression in factored form:

Therefore, .