Binomial Distribution

1. Binomial Distibution

Binomial distribution is a probability distribution that follows the binomial setting. A scenario can be considered binomial if it fits these four criteria:

1. The chance experiment has a fixed number of trials (n), with only two outcomes for each trial, denoted as "success" and "failure."
2. Each trial is independent of any others. So die rolling, coin flipping, spinning a spinner, all of those are independent events.
3. There has to be a fixed probability of success on every trial (p).
4. The variable of interest (what you’re interested in measuring) is the number of "successes." Typically, this is denoted as either r or k. We will use the letter k in this tutorial.

Also, you can rig the scenario to have two outcomes, even if there aren't technically two outcomes. For instance, on a die, there are six outcomes, but perhaps you could call rolling a 5 a success and anything but a 5 a failure. In that case, you've rigged it so you get two outcomes per trial.

EXAMPLE

One way to look at this is following the betting of black on a roulette wheel. Recall that there are 18 black sectors of the total 38 sectors on a roulette wheel.

Assume the gambler bets "black" four times in a row. He might win every time, which would be pretty lucky. However, he might lose every time. The following tree diagram shows all possible outcomes for betting four times on a roulette wheel.

Follow all the different scenarios:

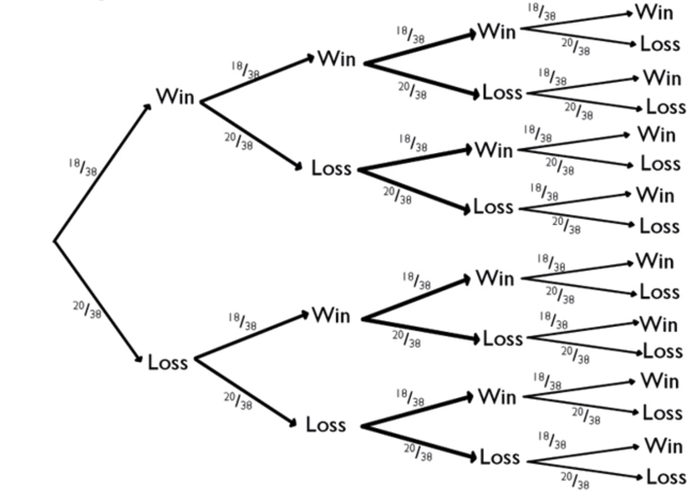
0 Wins
1 Outcome

He might lose all four times, and that would be no fun for him. There's only one way to do that--lose, lose, lose, and lose.

1 Win
4 Outcomes

He might win exactly one time as well. If you take a look above, there are four ways to do that.

Notice that all of these four branches on the tree diagram have the same probabilities on them--18/38 appears once, and 20/38 appears three times on each of these four branches.

2 Wins
6 Outcomes

He could also win twice. There are six ways to do that. He could win twice in a row, then lose twice in a row or he could lose-win, lose-win. Notice that regardless of which yellow branch you travel, 18/38 appears twice, and 20/38 appears twice.

3 Wins
4 Outcomes

They might also win three times. If you can see what we're going for--18/38 appears three times and 20/38 appears once. That happens on four branches of the tree diagram.

4 Wins
1 Outcome

Finally, the most fun scenario for the gambler: four wins. Now, 18/38 appears four times, and 20/38 doesn't appear at all, but that only happens one way.

Let's summarize all of this in a probability distribution.

Number of Wins	Probability	Explanation
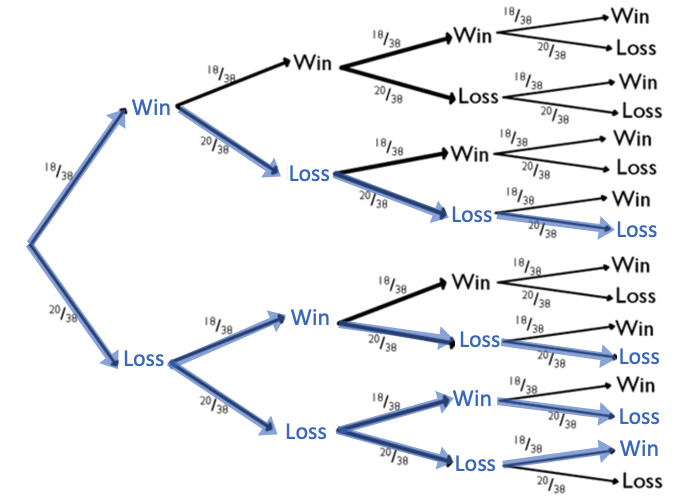
0		Zero wins only happened once. On that branch, 20/38 appeared four times in a row and 18/38 did not appear at all.
1		1 win happened four times. On each of those four branches, 20/38 appeared three times and 18/38 appeared once.
2		2 wins happend six times. On each of those six branches, 20/38 appeared twice and 18/38 appeared twice.
3		3 wins happened four times. On each of those four branches, 18/38 appeared three times and 20/38 appeared once.
4		4 wins only happened once. On that branch, 18/38 appeared four times in a row and 20/38 did not appear at all.

Look at the similarities and differences within these boxes. They all have the number of ways that these events happened: 0 wins happens once, 1 win happens four times, etc. In addition, they all have an 18/38. The first one (zero wins) has 18/38 to the 0 power. One win has 18/38 to the first power, two wins has 18/38 to the second power, and so on. Notice that's the same 0, 1, 2, 3, and 4 as the number of wins. So, trying to find the number of "k" wins, it will be 18/38 to the power of k.

You may also notice a pattern with the probability of losses. With four turns, or trials, one win had three losses; two wins had two losses, three wins had one loss, etc. You may notice that the wins and losses in each turn add up to the total number of trials. We can say that if there are "k" success in "n" trials, this means there are "n-k" failures.

Based on these similarities, there is a way to calculate the probability of winning a certain number of games.

formula to know

Binomial Distribution

The formula is denoted as: "n, choose k" times the probability of success to the power of k (which means you want to succeed k times out of n times), times the probability of failure (1 minus p) to the power of the rest of the trials that weren't successes, n minus k.

"N, choose k" is sometimes notated subscripted _nC_k. It's a number of ways to achieve k successes out of n trials. One way to find this amount is by creating a tree diagram and counting up the number of ways. However, if you're using a calculator, most calculators use the command _nC_r.

term to know

Binomial Distribution

The distribution of the number of successes that occur within n independent trials of a chance experiment with two outcomes per trial and p probability of success per trial.

2. Example

try it

What's the probability the gambler breaks even on four turns, meaning he wins twice and loses twice? Recall that our gambler always bets on black, which has a probability of 18/38.

Using the binomial distribution formula, we need to find k, n, and p and substitute in these values.




In four trials, 18/38 is the probability of winning. We knew from our tree diagram that there were six possible ways, which is equivalent to "4, choose 2". Put all those values in, and you get about a 37% chance of breaking even.

try it

Five dice are rolled. What's the probability of obtaining no more than one 5. Now, no more than one 5 could be either zero 5's or one 5. What you need to actually do this time is find the probability that you get no 5's, and add it to the probability that you get exactly one 5.



The probability of getting exactly zero 5s is 0.402.



The probability of getting exactly one 5 is 0.402.

As it turns out, just by sheer coincidence, they're the same number. So, the combined probability of getting no more than one 5 is 0.804.