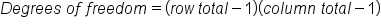EXAMPLE
Suppose that two colleges, the U and State, are worried about the student drinking behaviors, so they both independently choose random samples of their students. The results of the drinking behaviors are given in the table here:
|
Drinking Level
|
The U
|
State
|
|
None
|
140
|
186
|
326
|
|
Low
|
478
|
661
|
1,139
|
|
Moderate
|
300
|
173
|
473
|
|
High
|
63
|
16
|
79
|
|
|
981
|
1036
|
2017
|
The question is, does there appear to be a difference with drinking behaviors between the two colleges? Obviously, those who drink a lot represent the lowest category in both schools, and those who drink a little represent the highest in both schools. Perhaps the schools are not that different. You can run a test, though, to make sure whether that's the case or to dispute whether that's the case.
Step 1: State the null and alternative hypotheses.
In the test for homogeneity, the null hypothesis is that they are the same distribution, or that the two sample distributions are not significantly different; the distribution of drinking levels is the same at the U as it is for State. The alternative hypothesis is that the two distributions are not the same.
- H0: The distribution of drinking levels is the same for The U as it is for State.
- Ha: The distribution of drinking levels is not the same for The U as it is for State.
- α: 0.05
Choose a significance level of 0.05.
Step 2: Check the conditions.
One of the conditions is going to be that the expected values are all greater than five. But the question is, how do you calculate expected values? You can't do the same thing you did in a goodness-of-fit test. Instead, you have to think about it a different way. Of the 2,017 students, 326 of them don't drink at all, which is equal to 16.2%.
|
Drinking Level
|
The U
|
State
|
|
None
|
140
|
186
|
326
|
|
Low
|
478
|
661
|
1,139
|
|
Moderate
|
300
|
173
|
473
|
|
High
|
63
|
16
|
79
|
|
|
981
|
1036
|
2017
|
The idea here is that if the two distributions were homogeneous, then it would be 16.2% at The U that don't drink at all and 16.2% at State that don't drink it all.
(0.162)(981) = 158.56 The U students expected to not drink at all
(0.162)(1036) = 167.44 State students expected to not drink at all
So we would expect 158.56 students from The U and 167.44 students from State that participated in this survey to be in the "None" row.
Take a look at how this was calculated:

When you calculated the expected value for "None" and The U, you divided 326 by 2017 to get the 16.2%, and then multiplied by 981. In other words, we multiplied the total of "None" by the total of "The U", and divide all that by the grand total.
In general, what we can say is that the expected values for each cell are going to be the row total times the column total over the grand total.
- Expected Value for Cell in Chi-Square Test for Homogeneity

From that, it's not too hard to create an entire table of expected values.
|
Observed Table
|
|
|
Expected Table
|
|
|
Drinking Level
|
The U
|
State
|
|
Drinking Level
|
The U
|
State
|
|
None
|
140
|
186
|
326
|
None
|
158.56
|
167.44
|
326
|
|
Low
|
478
|
661
|
1139
|
Low
|
553.97
|
585.03
|
1139
|
|
Moderate
|
300
|
173
|
473
|
Moderate
|
212.54
|
224.46
|
473
|
|
High
|
63
|
16
|
79
|
High
|
38.42
|
40.58
|
79
|
|
|
981
|
1036
|
2017
|
|
981
|
1036
|
2017
|
The table on the left is what you observed; the table on the right is what you expected. Again, these values don't have to be integers.
The conditions for this hypothesis test are met: you have two independent random samples and all cell counts in the expected table are at least five, the smallest one being 38.42.
Step 3: Calculate the test-statistic and p-value.
At this point, you can calculate the chi-square statistic using the observed and expected. Recall that the formula for a chi-square statistic the observed minus expected, squared, over expected. Add all of them up.
- Chi-Square Test

You can also use technology to calculate the chi-square test statistic and the p-value.
The chi-square test statistic that you would obtain is 96.6.
The degrees of freedom, in this case, can be found by multiplying the number of rows minus one times the value of the number of columns minus one. This is technically the general rule and can be applied to the previous chi-square tests.
- Chi-Square Test Degrees of Freedom
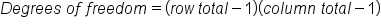
Let's take another look at our data:
|
Drinking Level
|
The U
|
State
|
|
None
|
140
|
186
|
|
Low
|
478
|
661
|
|
Moderate
|
300
|
173
|
|
High
|
63
|
16
|
In this case, there were four rows (none, low, moderate, and high) and two columns (The U and State):

So, the degrees of freedom is going to be equal to three. The chi-square statistic and p-value can all be obtained using technology and we get a corresponding p-value of 0.001. This is a very low value, less than 0.05.
Step 4: Compare your test statistic to your chosen critical value, or your p-value to your chosen significance level. Based on how they compare, state a decision about the null hypothesis and conclusion in the context of the problem.
Since the p-value is lower than the significance level, you reject the null hypothesis and conclude that there is a difference in drinking behavior between the students at the U and the students at State.