Table of Contents |
To begin, think back to the first four steps of the experimental method. Step 1 is choosing two different things you think might have some sort of cause-and-effect relationship. The second step is identifying how the two things might be related, or how the cause might affect the variable.
Step 3 is predicting how changing one variable will affect the other. The fourth step is experimenting with or testing the prediction by trying to determine if what you’re looking at has the predicted cause-and-effect relationship. To test your prediction, you will collect data. Collecting data on all members of a group is often impossible, inconvenient, and expensive. Consequently, you usually collect data on a portion of the group and use that information, along with statistical methods, to make inferences about the larger group.
IN CONTEXT
Say you suspect studying has a positive effect on test scores. You determine the relationship you think exists between studying and test scores and predict the effect. In Step 4, you test the prediction. What you’re doing is establishing that you think the more hours one studies for an exam, the better they’re going to do on it. You’re trying to see if the actual outcome is as predicted.
You could gather data on the number of hours students study for an exam. Then, look at their resulting exam scores to see if the number of hours spent studying increased exam scores. That would be an example of applying Step 4 of the experimental method.
You might guess that students who choose to study more may also be more likely to attend lectures and office hours and that these differences could also explain better test scores. This is called selection bias and was discussed in a previous tutorial. To address selection bias, it is best to randomly assign students with different amounts of study time and prescribe specific study activities.
In statistics, the goal is to determine information about an entire group of individuals or items. The problem is that this type of information is often difficult or even impossible to obtain. It is much easier to gather data from a small set of individuals or items that have characteristics similar to those in the larger group. Doing this enables us to make predictions regarding how the larger group will behave.
A population is an entire group of individuals or items that a researcher is interested in. Depending on the circumstances, the population could be an entire country or even the entire world. It could even be all plants or animals. Often, the population is a group, individuals, or items with a specific characteristic of interest, such as all people with a specific level of education or all houses that have four bedrooms.
Generally speaking, populations are likely very large, making it impossible or very costly to obtain information about each individual in the population. Because of this, a researcher typically chooses a much smaller group from the population. This group is called a sample.
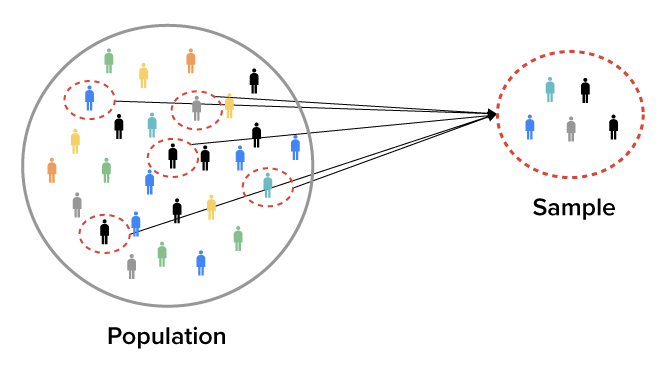
The researcher obtains the data from the sample, not the population. However, the sample should be representative of the population as a whole. If the sample is not representative of the population, then any conclusions drawn from the sample cannot be applied to the population, and the data is useless for estimating a specific aspect of the population.
IN CONTEXT
To get an idea of this, think about polling data that takes place around elections. The idea behind polling data is to take a sample of people who are registered or likely voters and get a sense of how they feel about a particular issue or candidate. This looks at a small sample that reflects the overall population as a whole.
You might ask 700 registered voters how they feel about a particular issue, or which candidate they prefer in this election. You would take that information from the sample and use it to make estimates about what the population itself looks like.
Source: THIS TUTORIAL WAS AUTHORED BY DAN LAUB FOR SOPHIA LEARNING. PLEASE SEE OUR TERMS OF USE.