Table of Contents |
The correlation coefficient, r, gives a general measure of strength and direction of a linear relationship. There is also the coefficient of determination, or r squared, which provides a very specific measurement. It provides the percent of the variation in the y-direction that can be explained by the linear relationship with the x variable. This can be a little confusing to understand.
EXAMPLE
Even though it is on the y-axis, the graph here is a dot plot of the seafood prices in 1980. This is going to be your y variable, but it's not very well contextualized. You would still wonder why the point all the way up at 400, which represents sea scallops, are so expensive. What would cause that to be so high, while other prices are so low?

Ultimately, r squared is always a positive number, and it does help to measure the strength of the linear association. It measures something very, very specific. It doesn't indicate the direction; it only can indicate the strength.
We can also use the coefficient of determination, r2 to find the correlation coefficient, r.
EXAMPLE
Look at each of the following examples and find the correlation coefficient, r, from r-squared.| Coefficient of Determination (r2) | Graph | Correlation Coefficient (r) |
|---|---|---|

|
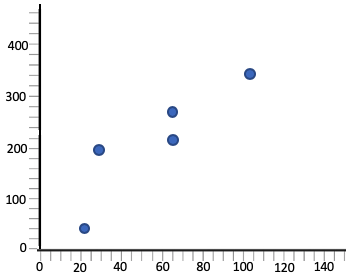
|
 Graph shows a positive association, so the correlation coefficient stays  . .
|

|
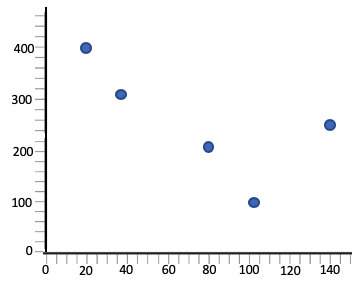
|
 Graph shows a negative association, so the correlation coefficient is actually  . .
|
Source: THIS TUTORIAL WAS AUTHORED BY JONATHAN OSTERS FOR SOPHIA LEARNING. PLEASE SEE OUR TERMS OF USE.