Table of Contents |
Solving an equation for a single variable is not always a single-step process. Often, complex expressions appear on either side of an equation, and it requires several steps to isolate the variable. It can save time and prevent confusion if you can simplify the expression by combining like terms before attempting to isolate the variable.
A term is a collection of numbers, variables, and powers combined through multiplication. Terms are referred to by their variable and power or exponent.
Consider the following expression with three terms:

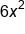 , can be read as 6 x squared, and is called an x-squared term. The 6 in front of the x squared is called a coefficient. The 2 is the exponent or power of the term.
, can be read as 6 x squared, and is called an x-squared term. The 6 in front of the x squared is called a coefficient. The 2 is the exponent or power of the term.  ).
).
Combining like terms is a method to simplify expressions before solving the equation using inverse operations. Terms may only be added or subtracted if they are like terms. Like terms are combined by adding or subtracting their coefficients and leaving the variable and exponent the same. A coefficient is the number that appears in front of a variable and acts as a factor or multiplier. Coefficients can be any real number, and terms without a written coefficient have an implied coefficient of 1, as illustrated here:

There are several common mistakes to avoid when combining like terms:
 , because the exponent does not change. Instead, 4x plus 3x means that you are adding 4 xs and 3 more xs, which equals a total of 7 xs. Thus, 4x plus 3x equals 7x.
, because the exponent does not change. Instead, 4x plus 3x means that you are adding 4 xs and 3 more xs, which equals a total of 7 xs. Thus, 4x plus 3x equals 7x.


EXAMPLE
Suppose you are simplifying the expression:

How would you combine like terms in a more complex expression with varying terms?
EXAMPLE
Combine like terms in the expression: .
.

|
Our Expression |

|
First, there are two x squared terms. The subtraction sign in front of the 2x squared makes the term negative. Combine -2x with 7x squared to get 5x squared. |

|
Next, we have three constant terms, 3, 11 and negative 4. Combine these terms to get 10. |

|
Our Simplified Expression |
A complex expression involving both varying terms and fractions requires several steps in the simplification process.
EXAMPLE
Suppose you want to simplify the expression: .
.

|
Our Expression |

|
There are two x cubed terms. These can be combined. Since the denominators are the same, we can add the numerators and keep the denominators. 1/5 and 1/5 equals 2/5x cubed. |

|
There are two x terms. Since the denominators are not the same, we need to find a common denominator. The least common denominator would be 4, so we can leave the fraction 4/3 unchanged, and multiply the fraction 1/2 by 2 in both the numerator and the denominator. |

|
Now that we have the same denominator, we can subtract 3/4x and 2/4x, which is 1/4x |

|
Our Simplified Expression |
Source: This work is adapted from Sophia author Colleen Atakpu.