Complement of an Event

1. Complement of an Event

Complement is not the same thing as saying something nice--this tutorial is discussing complement with an "e." Complement of an event, in a mathematical sense, is actually just the event not happening.

Look at the roulette wheel and find the probability that you'll land on a green sector when you throw the ball in there.

There are two green sectors out of 38, all of which are equally likely. The probability of landing on green is 2/38.

What about the probability of getting something that isn't green? Count everything that's not green, and you end up with 36 outcomes, or 36 out of 38. It seems like there's a relationship between those two numbers.

An event not occurring is called a complement of an event. For instance, the complement of the event landing in a green sector on the roulette wheel is the event landing in a sector that's not green.

big idea

There are many different ways to notate this.

If you write this A with an apostrophe, it’s called A prime. You can also use a bar, or you can use a c that looks like an exponent. You can also use a tilde (~). There's not a lot of consistency among different textbooks or among the mathematical community.

Looking back to the roulette wheel, the probability of landing on green was two out of 38. The probability of the complement of green, which was landing on anything besides green --denoted as P(green^c)-- was 36 out of 38.

The probability of the complement of an event is 1 minus the probability of the event.

formula to know

Complement of an Event

}}

IN CONTEXT

To find the probability of the complement of each of these events, you'd want to find the probability of the event first, and then subtract from one.

Event	Probability of Event	Probability of Complement
Rolling a "6" on a Die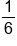
Spinning "Red" on a Roulette Wheel
Flipping "Tails" on a Fair Coin

term to know

Complement of an Event

All outcomes not in the given event.

2. Probability of "At Least One"

Suppose you flip a coin ten times. What's the probability that at least one of these flips is a head? Think about it using complements. What would be the complement of getting at least one head? The complement event would be getting no heads.

The probability of no heads is so much easier to calculate than the other one. When flipping a coin ten times, the probability of getting no heads is 1 out of 1,024 (for this specific problem, you don't need to know how to calculate that).

Therefore, the probability of at least one heads coming up on ten flips is 1 minus the probability of no heads, so 1,023 out of 1,024.

This leads us to an important finding within the context of real-life problems. Whenever you're asking for the probability of at least one, meaning something happens at least once, it's 1 minus the probability that it doesn't happen at all. At least once and not at all are complementary events. Probability of at least one is 1 minus the probability of none.

formula to know

Probability of "At Least One"