Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Completing the Square

Author: Sophia
PDF Version

what's covered
In this lesson, you will learn how to determine an equivalent quadratic equation by completing the square. Specifically, this lesson will cover:

Table of Contents

1. Solving a Quadratic in the Form (x + a)2

Some quadratic equations are difficult to solve, and some quadratic equations are easy to solve. Depending on how the equation is provided, certain methods can be very straightforward.

EXAMPLE

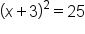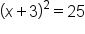
Find the solutions for quadratic equation open parentheses x plus 3 close parentheses squared equals 25.

We can find solutions to x by performing inverse operations, just like we solve other multi-step equations:

open parentheses x plus 3 close parentheses squared equals 25 Take square root of both sides
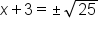
x plus 3 equals plus-or-minus square root of 25 Simplify square root
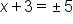
x plus 3 equals plus-or-minus 5 Subtract 3 from both sides
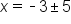
x equals short dash 3 plus-or-minus 5 Create two solutions, one with addition and one with subtraction
x equals short dash 3 minus 5 comma space space space x equals short dash 3 plus 5 Evaluate
x equals short dash 8 comma space space space x equals 2 Our solutions

Unfortunately, not all quadratic equations come in this form. However, we can manipulate the equation to write it as such. This requires a process known as completing the square.

2. FOIL & Completing the Square

To understand the mechanics of completing the square, it is helpful to connect it to the FOIL process. Let's take the general expression open parentheses x plus a close parentheses squared and FOIL it:

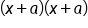
open parentheses x plus a close parentheses squared Multiply two factors of open parentheses x plus a close parentheses
open parentheses x plus a close parentheses open parentheses x plus a close parentheses FOIL
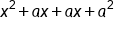
x squared plus a x plus a x plus a squared Combine like terms
x squared plus 2 a x plus a squared Our solution

big idea
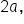The coefficient of the x-term is 2 a comma and the constant term is a squared. If we can manipulate an expression to be in the form x squared plus 2 a x plus a squared, then we can write it equivalently as open parentheses x plus a close parentheses squared. This is the goal of completing the square.

term to know
Completing the Square
The process of converting a quadratic equation in the form a x squared plus b x plus c equals 0 into an expression involving a perfect square trinomial.

3. Solving a Quadratic by Completing the Square

The process of completing the square follows a specific set of steps in order to convert the equation into one similar to our very first example:

step by step
  1. Move the constant term to the other side of the equation.
  2. Divide the entire equation by the x-square coefficient.
  3. Separately, divide the x-term coefficient by two, then square it.
  4. Add this quantity to both sides of the equation.
  5. Write one side of the equation from expanded form into factored form, expressed as a single factor squared.

Let's apply these steps to the following example.

EXAMPLE

Rewrite 2 x squared minus 12 x minus 14 equals 0 by completing the square.

2 x squared minus 12 x minus 14 equals 0 Move the constant term, 14, to the other side by adding 14 to both sides
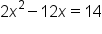
2 x squared minus 12 x equals 14 Divide entire equation by the x-square coefficient, 2
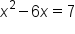
x squared minus 6 x equals 7 Separately, divide the x-term coefficient, 6, by two, then square it
short dash 6 rightwards arrow fraction numerator short dash 6 over denominator 2 end fraction equals short dash 3 rightwards arrow open parentheses short dash 3 close parentheses squared equals 9 Add this value, 9, to both sides
x squared minus 6 x plus 9 equals 7 plus 9 Simplify the right side
x squared minus 6 x plus 9 equals 16 Rewrite left side as binomial squared
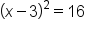
open parentheses x minus 3 close parentheses squared equals 16 Equivalent equation to 2 x squared minus 12 x minus 14 equals 0

The last step is a bit tricky. We were able to write the right side of the equation as a binomial squared, because of the relationship between the coefficients and the constant term. When -3 is doubled, it is equivalent to the x-term coefficient in expanded form, -6, AND when it is squared, it equals to constant term in the expanded form, 9.

Now that we have converted an equation from standard form into a binomial squared, we can solve this equation following the same procedure as our very first example:

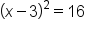
open parentheses x minus 3 close parentheses squared equals 16 Take square root of both sides
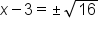
x minus 3 equals plus-or-minus square root of 16 Simplify square root
x minus 3 equals plus-or-minus 4 Add 3 to both sides
x equals 3 plus-or-minus 4 Create two solutions, one with addition and one with subtraction
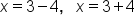
x equals 3 minus 4 comma space space space x equals 3 plus 4 Evaluate
x equals short dash 1 comma space space space x equals 7 Our solutions

summary
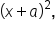When solving a quadratic in the form (x + a)2, we can find the solutions by performing inverse operations. FOIL and completing the square is a method of solving a quadratic equation. Solving a quadratic by competing the square involves rewriting a quadratic equation as a perfect square trinomial so that it can be written in factored form as open parentheses x plus a close parentheses squared comma where a and y are real numbers.

Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License

Terms to Know
Completing the Square

The process of converting a quadratic equation in the form a x squared plus b x plus c equals 0 into an expression involving a perfect square trinomial.

© 2024 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.