Table of Contents |
A complex number is a number in the form  , containing both a real part and an imaginary part. The imaginary part is followed by
, containing both a real part and an imaginary part. The imaginary part is followed by  , which is the imaginary unit,
, which is the imaginary unit,  .
.
One application of complex numbers is in electrical engineering (as well as other engineering and scientific fields). Complex numbers occur in calculations involving electrical currents, which will be explored in the examples below. Depending on the situation, we will need to either multiply or divide two complex numbers. During these processes, we use FOIL and complex conjugates to find our solutions. Let's briefly review the FOIL process and complex conjugates.
FOIL stands for First, Outside, Inside, Last, and refers to the terms that are multiplied together to form individual addends to the product.
EXAMPLE
Multiply

|
Multiply first terms: 
|

|
Multiply outside terms: 
|

|
Multiply inside terms: 
|

|
Multiply last terms: 
|

|
Combine like terms |

|
Our solution |
 term. This simplifies to a real number because
term. This simplifies to a real number because 
When dividing two complex numbers, we use the denominator's complex conjugate to create a problem involving fraction multiplication. A complex number and its conjugate differ only in the sign that connects the real and imaginary parts. Here is a table of complex numbers and their complex conjugates.
| Complex Number | Complex Conjugate |
|---|---|

|

|

|

|

|

|

|

|
When working with electrical circuits, electrical engineers often apply the following formula to relate voltage, current, and resistance:
 , where
, where 
 instead of
instead of  , so as not to confuse the imaginary unit with the variable for current. So keep in mind in these examples that whenever we see
, so as not to confuse the imaginary unit with the variable for current. So keep in mind in these examples that whenever we see  , this represents our imaginary unit, and has a value of
, this represents our imaginary unit, and has a value of  .
. , this variable is also often written before its coefficient, rather than after. For example the complex
, this variable is also often written before its coefficient, rather than after. For example the complex  number might be written as
number might be written as  .
.If we are finding the voltage, V, we will multiply the current, I, by the resistance, R.
EXAMPLE
An electrical circuit has a current of amps, and a resistance of
amps, and a resistance of  ohms. What is the voltage of the circuit?
ohms. What is the voltage of the circuit?


 and
and  are interchangeable, so we can replace all instances of
are interchangeable, so we can replace all instances of  with
with  when multiplying. So
when multiplying. So  can be written as
can be written as  and
and  can be written as
can be written as  .
.


|
Multiply first terms: 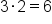
|

|
Multiply outside terms: 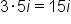
|
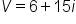
|
Multiply inside terms: 
|
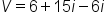
|
Multiply last terms: 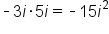
|
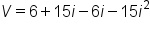
|
Combine like terms |
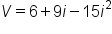
|
Rewrite 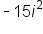 as +15 as +15
|

|
Combine like terms |
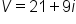
|
Our solution |
 volts.
volts.
Suppose we need to find the current, I. We can divide the voltage, V, by the resistance, R.
EXAMPLE
An electrical circuit has a voltage of volts, and a resistance of
volts, and a resistance of  ohms. What is the circuit's current?
ohms. What is the circuit's current?


 instead of
instead of  :
:


|
Multiply by a second fraction with the conjugate  in the numerator and denominator in the numerator and denominator
|

|
Multiply the two fractions |

|
Use FOIL to evaluate numerator and denominator |

|
Combine like terms in numerator and denominator |

|
Rewrite  as as  and and  as as 
|

|
Combine like terms in numerator and denominator |

|
Separate into two fractions |

|
Simplify fractions |

|
Our solution |
 amps.
amps.
 and an imaginary part, b, and the imaginary unit, i. Reviewing FOIL and conjugates, the conjugate of a binomial is a binomial with the opposite signs between its terms.
and an imaginary part, b, and the imaginary unit, i. Reviewing FOIL and conjugates, the conjugate of a binomial is a binomial with the opposite signs between its terms.
Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License