Table of Contents |
Financial accounts appreciate in value according to an annual interest rate, which we typically refer to as APR (annual percentage rate). When using the APR to calculate account balances with interest, we always express the percentage as a decimal.
EXAMPLE
A 5% APR would be expressed as 0.05.When multiplying an account balance by its growth factor according to interest, we can generally say that the growth factor is  , where r is the ARP expressed as a decimal. We add 1 to r, because the new account balance includes 100% of the original balance, plus any interest gained.
, where r is the ARP expressed as a decimal. We add 1 to r, because the new account balance includes 100% of the original balance, plus any interest gained.
If interest is applied only once per year, we can multiply this growth factor of  by the initial account balance after each year, leading to the annual interest formula:
by the initial account balance after each year, leading to the annual interest formula:
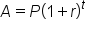
In this formula,
Many accounts gather interest several times per year, not just once. This is compounding interest. When interest is compounded, a portion of the APR is applied throughout the year.
Our formula for compounding interest is:
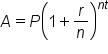
In this formula:
Now that we have a formula to work with, we can use this formula to answer questions about account balances, provided we have information about APR and how many times per year the interest is compounded. Consider the following scenario asking us to find the balance of an account after a certain time period.
EXAMPLE
A checking account has an initial balance of $800.00. The account gains 3.5% interest, which is compounded monthly. What is the value of the account after 4 years, assuming no additional withdrawals or deposits are made?
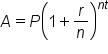
|
Plug in 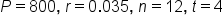
|
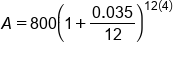
|
Evaluate the division in the parentheses |
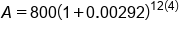
|
Simplify the parentheses |

|
Evaluate exponent |

|
Apply exponent |
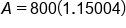
|
Multiply |
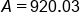
|
Our solution, rounded to the nearest cent |
In this next sample, we are going to see how to apply logarithms to solve for the variable time, t.
EXAMPLE
Using the same account from above, that has an initial balance of $800.00 with 3.5% interest compounding monthly. We would like to know how many years it will take for the account balance to double.
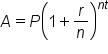
|
Plug in 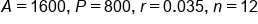
|
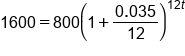
|
Simplify parentheses |
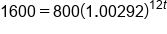
|
Divide both sides by 800 |

|
Solve for t |

|
Take log of both sides |

|
Apply Power Property of Logs |
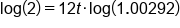
|
Divide both sides by 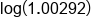
|
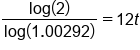
|
Use a calculator to evaluate the division on the left side |

|
Divide both sides by 12 |
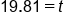
|
Our solution |
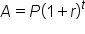 . In the compound interest formula, A is the account balance, P is the principal, r is the annual interest rate, n is the number of times per year that the interest is compounded, and t is the time in years. Compounding interest means that a portion of the annual interest rate is applied throughout the year. When solving for the account balance, we are solving for the variable A. When solving for the growth time, we are solving for the variable t and will need to apply a logarithm.
. In the compound interest formula, A is the account balance, P is the principal, r is the annual interest rate, n is the number of times per year that the interest is compounded, and t is the time in years. Compounding interest means that a portion of the annual interest rate is applied throughout the year. When solving for the account balance, we are solving for the variable A. When solving for the growth time, we are solving for the variable t and will need to apply a logarithm.
Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License