Determine an Equation in Context

1. The Meaning of Certain Words in Math

Word problems can be tricky. Often it takes a bit of practice to convert the English sentence into a mathematical sentence. This is what we will focus on here with some basic number problems, geometry problems, and parts problems. A few important phrases are described below that can give us clues on how to set up a problem.

Word to Math Phrases	Examples
A number (or unknown, a value, etc.) often becomes our variable	If you want to find the number of books you bought, you may use the variable b in your problem.
"Is" (or other forms of "is": "was", "will be", "are", etc.) often represents equals (=).	"x is five" becomes
"More than" often represents addition and is usually built backwards, writing the second part plus the first.	"Three more than a number" becomes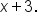
"Less than" often represents subtraction and is usually built backwards as well, writing the second part minus the first.	"Four less than a number" becomes
The product of two numbers often represents multiplication between two quantities.	"The product of two unknowns is 5" means that we have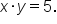
The quotient of two numbers often represents division between two quantities.	"The quotient of a number and 5 is 4" can be written as

2. Single-Step Equations

Using these key phrases, we can take a number problem and set up an equation and solve.

EXAMPLE

Suppose we were told Rachel earned $40,000 a year for some number of years and ended up making a total of $280,000 over that time period. For how many years did Rachel work? Can you determine an equation to represent the problem and solve the equation?

Here, we know how much Rachel earns each year, but we are told that this was for "some number of years," which alerts us that the number of years worked would be a variable. We can also think that if we multiply the number of years worked by her salary each year, we can set that number equal to the total amount earned. Using this equation, we can then solve the problem.

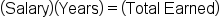
	Create an equation. Substitute given information, ,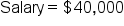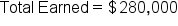
	Solve for years, y, by dividing both sides by 40,000
	Our Solution

Rachel worked for 7 years, earning $40,000 a year, and earned a total of $280,000.

3. Multi-Step Equations

Using these key phrases, we can take a number problem and set up an equation and solve.

EXAMPLE

If 28 less than five times a certain number is 232, what is the number?

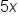
	We know that we are multiplying a certain number by 5, so we'll start with 5x. We also know that we are taking 25 from that 5x, so subtract 25 from 5x
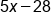
	"Is" translates to "equals" so include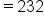
	Now we can solve this equation by first adding 28 to both sides
	Divide both sides by 5
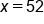
	Our solution

This same idea can be extended to a more involved problem as shown in the next example:

EXAMPLE

Seventeen more than three times a number is the same as ten less than 6 times the number. What is the number?

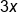
	We know that we are multiplying a certain number by 3, so we'll start with 3x. We also know that we are adding 17 more to this value, so add 17 to 3x
	"Is" translates to "equals" so include an equal sign
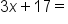
	Now find the second part. We know we are multiplying that same number by 6, so include a 6x
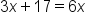
	We also know that we are taking 10 from that 6x, so subtract 10 from 6x
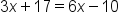
	Now we can solve this equation by first subtracting 3x from both sides
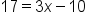
	Add 10 to both sides
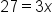
	Divide both sides by 3
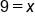
	Our solution

4. Solving Problems in Context

When working with word problems, it is always a good idea to start by clearly labeling the variables in a short list before we begin to solve the problem. This is important in all word problems involving variables, not just consecutive numbers or geometry problems.

EXAMPLE

A sofa and a loveseat together cost $444. The sofa costs double the love seat. How much do they each cost?

	Together, the sofa and loveseat cost $444, which gives us this equation. With no other information about the loveseat, this becomes our variable, which we'll call x.
	We know the sofa is double the loveseat, so we multiply x by 2
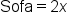
	Replace these values in the original equation
	Combine like terms, x and 2x
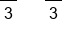
	Divide both sides by 3
	Our solution for x, which we gives us the cost of the loveseat
	Now find the cost of the sofa by substituting the cost of the loveseat
	Evaluate
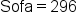
	The cost of the sofa

The loveseat costs $148 and the sofa costs $296, for a total of $444.

hint

Be careful on problems such as these. Many students see the phrase "double" and believe that it means we only have to divide 444 by 2 and get for one or both of the prices. As you can see, this will not work. By clearly labeling the variables in the original list, we know exactly how to set up and solve these problems.