Determining Intercepts

1. Determining Intercepts on a Graph

When we talk about a line's intercepts, we most often mean the x-intercept and the y-intercept. These are locations where the line intercepts or crosses the x- or y- axis. A Below is the graph of a line, with both intercepts shown:

big idea

Notice that the x-intercept always has a y-coordinate of 0, and the y-intercept always has an x-coordinate of 0.

terms to know

x-intercept

Where a line or curve intersects the x-axis, at

y-intercept

Where a line or curve intersects the y-axis, at

2. Determining Intercepts from a Table

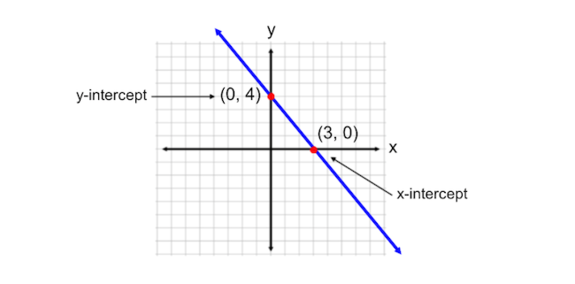
Keeping the above note in mind, we can easily identify intercepts from a table of x and y values when we notice that one of the coordinates is zero!

EXAMPLE

Find the x-intercept and y-intercept for the list of values in the following table.

x	y
-2	18
0	12
2	6
4	0
6	-6

We see that a coordinate pair (0, 12) contains a zero. In this coordinate pair, the x-coordinate is zero, which means this actually represents the y-intercept. The y-intercept of the line is at the point (0, 12).

We also notice a zero in the coordinate pair (4, 0). In this case, the y-coordinate is zero, so this is the x-intercept. The line crosses the x-axis at the point (4, 0).

3. Determining Intercepts from an Equation

How can we use the equation of a line to find its x- and y- intercepts? A common form of a line is in slope-intercept form: 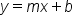. This form is called slope-intercept form because b represents the y-coordinate of the y-intercept (and we know that its x-coordinate is 0). We can also use the equation in this form to find the x-intercept. Since x-intercepts have a y-coordinate of 0, we set the equation equal to zero and solve for x.

EXAMPLE

Find the x-intercept and y-intercept of the equation .

We can easily find the y-intercept:

	When we have the equation in the form 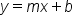, the variable b is the y-coordinate of the y-intercept
	This is the y-coordinate of the y-intercept. For the y-intercept, the x-coordinate is always 0
	The y-intercept is (0,8)

Now, find the x-intercept:

	To find the x-intercept, plug 0 in for y as the y-coordinate is always 0
	Subtract 8 from both sides
	Divide both sides by -2
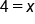
	This is the x-coordinate of the x-intercept. For the x-intercept, the y-coordinate is always 0
	The x-intercept is (4,0)

For the equation , the x-intercept is at (4,0) and the y-intercept is at (0,8).