Determining Slope

1. Algebraic Definition of Slope

The slope of a line measures its steepness. A common way to think about the slope of a line is the "rise over run." This means that we calculate a change in a vertical position from one point to another, and divide it by the change in the horizontal position between those two points. Algebraically, we have the following formula for slope:

formula to know

Slope

The numerator of the fraction, or the "rise", is the difference in y-coordinates from two points on the line, and the denominator of the fraction, or the "run", is the difference in x-coordinates from the same two points on the line. As we can see in our formula, all that is needed to calculate the slope of a line are the coordinates of two points on the line.

2. Finding Slope from Two Points

Let's find the slope of a line that passes through two points

EXAMPLE

Find the slope of the line that passes through (-2, 6) and (4, 18).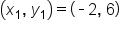

First, we need to define each point as Point 1 and Point 2, so that the x- and y-coordinates are used in the correct order in our formula. We will define Point 1 as and Point 2 as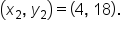

To find the slope of the line that passes through (-2, 6) and (4, 18), the process is as follows:

	Use the slope formula and substitute the known values: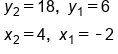
	Simplify the numerator and denominator
	Divide 12 by 6
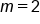
	Our Solution

hint

It does not matter if we had decided to label Point 1 as (4, 18) and Point 2 as (-2, 6), our calculation for slope will be the same. The important thing is to be consistent with which coordinates are subtracted in our calculation. For example, (y₁ – y₂) / (x₁ – x₂) would give the same result.

3. Finding Slope from a Table of Values

If we are given a table of values that represent different x- and y-coordinate pairs to a line, we can calculate the slope of the line by choosing any two coordinate pairs, and plugging them into the formula for slope.

EXAMPLE

Find the slope of the line associated with the values in the following table.

x	y
4	11
6	25
8	39
10	53

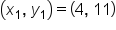Remember, all we need is two points to calculate the slope of the line. We can choose any two rows here to represent x- and y-values to use in our formula. To show the solution, let's choose the first and last sets of values: and

	Use the slope formula and substitute the known values: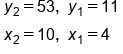
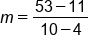
	Simplify the numerator and denominator
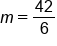
	Divide 42 by 6
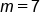
	Our Solution

summary

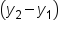The algebraic definition of slope is m equal divided by 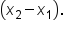The slope of a line is commonly referred to as the rise over run, with the rise is the difference in y-coordinates, and the run is the difference in x-coordinates between any two points on a line. To determine the slope, you only need the x and y-coordinates from two points or a table of values.