Distance, Rate, and Time

1. Relationship between Distance, Rate, and Time

An application of linear equations can be found in distance problems. When solving distance problems we will use the relationship 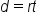or distance equals rate (speed) times time.

formula to know

Distance, Rate, Time

There are a couple of ways we can represent this relationship:

Formula	Solve for...
	distance
	rate
	time

2. Solving an Equation for Distance

The first example on how to use the distance-rate-time relationship is solving for distance.

EXAMPLE

Jason ran for 45 minutes, or 0.75 hours, at a speed of 7 miles per hour. How far did he run?

We want to know how far he ran so that going to be the distance. We can see that the rate is going to be 7 miles per hour and the time is going to be 0.75 hours. We can use the following equation:

Using this formula, we are going to multiply the rate, which is 7 miles per hour, or 7 miles over 1 hour, by the time, which is 0.75 hours, which can be written as 0.75 hours over 1.

Remember from doing unit conversions, when we want to figure out our units, the goal is to get units to cancel. We can see that hours in the denominator and hours in the numerator are going to cancel out. So the answer is going to be in terms of miles, which is good since we are trying to find the distance.

We just need to multiply and simplify the fractions. Multiplying 7 times 0.75 equals 5.25 and the 1 in the denominator simply cancels out because any value divided by 1 is just the value itself.

Running for 45 minutes, or 0.75 hours, at a speed of 7 miles per hour, Jason ran a total distance of 5.25 miles.

3. Solving an Equation for Rate

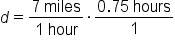
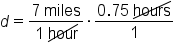
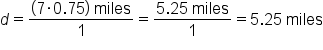
In this second example, we'll solve for rate.

EXAMPLE

Lee biked to his friend's house in 2 hours. He knows that his friend's house is 42 miles from where he started and he wants to know how fast did he bike.

Finding how fast Lee bikes is going to be a rate. We know that the distance is 42 miles and the time is 2 hours. So we can use this formula for the rate, which is equal to distance over time.

We can start by substituting the value for distance, 42 miles, and the value for time, 2 hours.

We can simplify these two numbers. 42 divided by 2 is going to equal 21. None of the units cancel out, so the units of the answer are going to be in terms of miles per hour.

Biking 42 miles in 2 hours, Lee's rate is 21 miles per hour.

4. Solving an Equation for Time

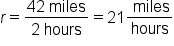
Finally, let's look at example where we solve for time.

EXAMPLE

Shira wants to rollerblade to the corner store. She knows she can rollerblade at 12 miles per hour and that the store is 4 miles away. How long will it take for her to get there?

We want to find out how long it will take, which means we want to find the time. We know the distance and the rate so we can use this formula for time, which again time is equal to the distance over the rate divided by the rate.

The distance is going to be 4 miles and the rate is going to be 12 miles per hour, or 12 miles in 1 hour.

If you notice, there is a fraction in the denominator. We can actually rewrite this using the reciprocal. The whole equation can be rewritten as 4 miles times 1 hour/12 miles, which still describes the speed. We can put 4 miles over 1 and see how the units cancel.

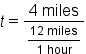
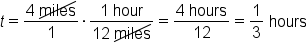
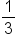So the miles in the numerator of the first fraction will cancel with the miles in the denominator of the second fraction. Now we are left with hours as the unit, which is good because we are trying to find time. 4 times 1 is 4. 1 times 12 is 12, and this reduces to . It will take Shira 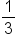hours. If we want this fraction in minutes, we can just multiply it by the conversion factor, .

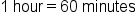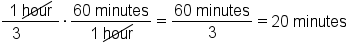
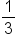It will take Shira hours, or 20 minutes, to rollerblade 4 miles at a rate of 12 miles per hour.