Table of Contents |
The general exponential equation is  , where a base number, b, is raised to a variable exponent power, x. There is also a scalar multiplier,
, where a base number, b, is raised to a variable exponent power, x. There is also a scalar multiplier,  in front of the exponential expression.
in front of the exponential expression.
Exponential growth can be modeled with a similar equation:
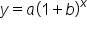
In this formula,
 is the initial value.
is the initial value.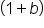 the growth factor, since it's multiplied by
the growth factor, since it's multiplied by  (the initial value) x number of times.
(the initial value) x number of times.
In 2000, the population of Berlin was about 3.39 million. The city's population has been growing at an average rate of 0.27% each year. Assuming this rate of growth remains the same, what is Berlin's expected population in the year 2050?
From the scenario, we can draw the following values for certain variables in the exponential growth formula:
 (expressed in millions, the population in the year 2000)
(expressed in millions, the population in the year 2000)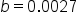 (0.27% expressed as a decimal)
(0.27% expressed as a decimal)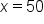 (50 years between 2000 and 2050)
(50 years between 2000 and 2050)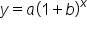 , to find the population after 50 years, y:
, to find the population after 50 years, y:

|
Plug in 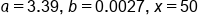
|
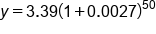
|
Simplify inside the parentheses |
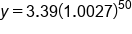
|
Apply exponent |

|
Multiply |
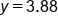
|
Our solution |
The expected population for Berlin in the year 2050 is about 3.88 million people.
We can also use the exponential growth formula to calculate for a period of time. A common application of exponential growth is the spread of viruses.
During the 14th century, the "Black Death" devastated the population of Europe. At its peak in 1350, the plague had infected 1.5 million in just two years. If the plague had continued to spread at a rate of 18.27%, how long would it have taken to infect 4 million people?
Looking at the exponential growth formula, we no longer have a known value for x, as x represents time. However, we can make the following substitutions:
 (expressed in millions, ending value)
(expressed in millions, ending value)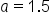 (expressed in millions, initial value)
(expressed in millions, initial value) 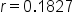 (18.27% expressed as a decimal)
(18.27% expressed as a decimal)

|
Plug in 
|

|
Simplify inside the parentheses |
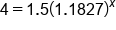
|
Divide by 1.5 |

|
Apply log to both sides |
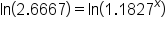
|
Apply Power Property of Logs |
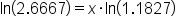
|
Divide both sides by 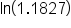
|
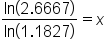
|
Evaluate fraction |

|
Our solution |
It would take about 5.8 years for the plague to infect 4 million people.
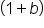 , not
, not 
 is the initial value and b is the rate of change expressed as a decimal. It is added it 1 to represent growth. When calculating a growth population, you are solving for y. When solving for growth time, you are solving for the variable exponent. One method is to take the log of both sides of the equation and apply properties of logs.
is the initial value and b is the rate of change expressed as a decimal. It is added it 1 to represent growth. When calculating a growth population, you are solving for y. When solving for growth time, you are solving for the variable exponent. One method is to take the log of both sides of the equation and apply properties of logs.
Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License