Finding the Domain and Range of Functions

1. Domain and Range

In a function, the domain is the set of all possible input values. In other words, it represents all values that the independent variable (usually x) is allowed to take on in order to return a value for the function. The range is the set of all possible output values (usually y); or values that the function will have, depending on all of the possible input values.

When a function has no restrictions on its domain, it is continuous from negative infinity to positive infinity along the x-axis. If the range also has no restrictions, then on one end, the graph tends towards negative infinity, and on the other end, it tends towards positive infinity. Below is the graph of a polynomial that has no domain or range restrictions:

When talking about domain restrictions, the two common cases:

• When there is an expression underneath a square root (or other even roots) because the expression under the even root must be non-negative
• When there is a denominator with a variable in it (as is the case with rational functions) because the denominator must not equal zero

terms to know

Domain

The set of input values of a function or relation.

Range

The set of output values of a function or relation.

2. Domain and Range of Square Root Functions

The find the domain range, we need to identify restrictions to both the domain and range.

EXAMPLE

Find the domain and range of .

Since this is a square root function, we need to set the expression underneath the radical, , greater than or equal to zero, and solve the inequality for x:

	Subtract 2 from both sides
	Divide by 4
	Simplify
	Our solution

This means that the function is defined for any x-value greater than or equal to negative one-half. We can write this as . We can see this below when we graph the function. If the inequality had no solution (that is, no values of x for which the expression is less than zero), then the domain has no restrictions.

Since this function does not have a denominator, we can simply examine the graph of this function to describe its range:



We see that as x gets larger and larger, the function heads towards positive infinity (even if rather slowly). On the other side of the graph, however, the function never falls below the x-axis. Therefore, the range is from zero to positive infinity. Since the function can have the exact value of zero, we can write this as

For the function , the domain is and the range is

big idea

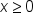For square-root functions, the range is any value of x such that . It is not possible for a square root to result in a negative value, so the functions in the form or will always be greater than or equal to zero.

3. Domain and Range of Rational Functions

With rational functions, the domain restrictions are x-values that make the denominator equal to zero. So we need to set the denominator equal to zero and solve for x. This will give us x-values to exclude from the domain:

EXAMPLE

Find the domain and range of .

To find the domain restrictions, set the denominator equal to zero and solve for x.

	Factor the quadratic expression
	Set each factor to zero
	Evaluate each factor
	Our solutions

This means that the domain of the rational function is all x-values EXCEPT and .

If we are able to rewrite the denominator in factored form, it is easier to see the solutions. In the above example, the function can be written as . Setting each factor in the denominator to zero will give the values of the restrictions. And as we said above, if the equation has no solution (that is, no values of x that make the denominator equal to zero), then the domain has no restrictions.

To find the range, we can examine the graph of this function, too:



We can see that the domain restrictions are represented with the vertical asymptotes in this function, at and .

We also see a horizontal asymptote, which can be found by dividing the leading coefficients in the numerator and denominator of the function. So the line is . We may be tempted to say that 2 is excluded from the range, because as the function gets more and more negative, and more and more positive, the value of the function approaches, but never reaches 2. However, in between our vertical asymptotes, we see that function actually does at one point have a value of 2. So we can then say that the range of this function is all real numbers,

For the function , the domain is all values of x EXCEPT for -1 and 2, and the range is all real numbers.