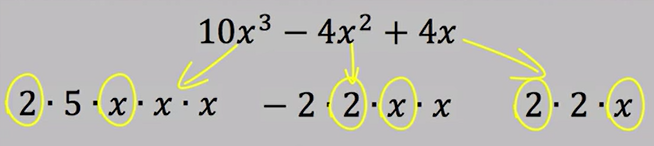This tutorial covers how to find the greatest common factor of a polynomial, through the definition and discussion of:
1. Factors and Terms in Polynomials
A polynomial is a mathematical expression involving one or more terms. Terms are separated by addition or subtraction, and each term may contain coefficients, variables, and exponents that are multiplied together.
-
EXAMPLE
The following polynomial has three terms:

In the first term, 7 is the coefficient, y is the base, and 4 is the exponent.
The coefficients and variables of a term are factors of that term. An expression can also be a factor of a polynomial if it is multiplied by another expression to get the original polynomial as a product.
-
EXAMPLE
In this expression, x minus 1 and 2x plus 5 are both factors of the polynomial.

2. Distribution and Factoring
Distribution involves multiplying a factor outside the parentheses by all the terms inside the parentheses.
As shown in the formula below, the a variable is multiplied by both the b and the c inside the parentheses.

Factoring, on the other hand, is the reverse process of distributing, in which a common factor is factored out of two or more terms, and written outside of the parentheses.
In the formula below, the variable a is the common factor of ab and ac. You can factor it out by writing it on the outside of the parentheses, and writing b plus c inside the parentheses.

3. Factorization
Being able to factor a polynomial is useful for:
- Simplifying polynomials
- Canceling common factors
- Identifying information, such as intercepts, on graphs
The process of finding common factors of a polynomial works in the same manner as finding common factors of numbers. To “factor” means to break down a number into smaller numbers that, when multiplied together, give you the original number.
-
EXAMPLE
The number 30 can be broken down into smaller numbers, as shown below. When multiplied together, these smaller numbers are equal to 30. These smaller numbers are also the prime factorization of 30, because 2, 3, and 5 are all prime numbers.

-
Writing the prime factorization of all terms in a polynomial helps identify common factors and the greatest common factor.
4. Factoring Polynomials
Suppose you want to factor the following polynomial. To do this, you need to factor or break down each individual term into its prime components.

Looking at these three factorizations, you can see that the common factor of each of these terms is 3. If terms have two or more common factors, the factors can be multiplied together to find the greatest common factor.
-
EXAMPLE
To factor the following polynomial, you need to find the prime factorization of each of the three terms.
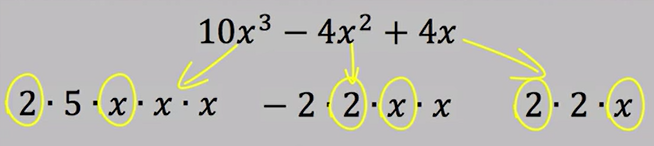
You can see that all of your terms have two common factors. They each have a positive 2, and they each have a variable x. To find your greatest common factor, you multiply these two common factors, 2 and x. Therefore, your greatest common factor is 2x.
Once you have factored out the greatest common factor, the expression inside the parentheses will be the remaining factors of each term. From your first term, your remaining factors are 5x and x or 5x^2. In your second term, the remaining factors are a -2 and x, or -2x. Finally, in your last term, the remaining factor is 2.

You can check to see that you have factored the polynomial correctly by distributing the greatest common factor back into each term inside the parentheses:

Because you have arrived back at your original expression, you have factored your polynomial correctly.
-
Consider the following expression:

Factor this expression. Remember, you’ll need to factor each of the three terms.Here, again, you see that you have two common factors in each term, as each term has a 2 and a 3.

Multiplying these common factors together provides your greatest common factor of 6. Since 6 is your greatest common factor, write it on the outside of the parentheses. Inside the parentheses, write the remaining factors of each term. Note that in your last term, you have already factored out both of the factors of 6, which means that you only have a 1 remaining.

Check to see that you have factored your polynomial correctly by distributing the 6 back into each of the three terms in the parentheses.

Since you have arrived back at your original expression, you have indeed factored your polynomial correctly.
Today you learned about factors and terms in polynomials, which are expressions involving one or more terms. You reviewed the process of distribution, and learned that factoring is the reverse process of distributing, in which a common factor is factored out of two or more terms and written outside of the parentheses. You also learned about factorization, and how finding the prime factorization of all terms in a polynomial helps identify common factors and the greatest common factor. Lastly, you learned how to apply all of this knowledge in factoring polynomials.