Table of Contents |
Consider the arithmetic sequence {3, 8, 13, 18, 23, 28}.
With only a few terms, it is easy enough to find the sum of all terms in this sequence. We can simply add the terms together to get a sum of 93. However, what if we had been given a sequence with 100 terms in it, and asked to find the sum? We still could add the terms concretely, but it would be inefficient. Let's take a look at an interesting shortcut.

|
Add the outermost terms: 3+28=31 |

|
Working our way in: 8+23=31 |

|
Further in: 13+18=31 |
There is an interesting pattern when we add the first and last terms together, and then work our way to the center of the sequence. In each case, the sum is the same, in this case, 31. Due to this pattern, we know that the sum of all of the terms is going to be a multiple of 31. How many times should we multiply 31? We saw that we formed 3 pairs of 31, so the sum of all 6 terms is 93. To generalize this pattern, we need to think about the relationship between 6 terms and 3 pairs that sum to the same value. Since we were pairing terms, there are exactly half as many pairs as there are terms.
In general, then, to find the sum of an arithmetic sequence, we can add the first term and the n-th term, and then multiply that by the number of terms, n, divided by 2. Here is what our formula looks like:

In this formula, we can define each variable as:
 : the sum of n terms
: the sum of n terms : the value of the 1st term
: the value of the 1st term : the value of the nth term
: the value of the nth term : the term
: the termEXAMPLE
Find the sum of the first 8 terms in the sequence:
 ) and the eighth term (
) and the eighth term ( ) to plug into our formula, which in this case are
) to plug into our formula, which in this case are  and
and 


|
Substitute  , ,  , , 
|

|
Add -8 and 34 |

|
Divide 8 by 2 |

|
Multiply 4 and 26 |

|
Our Solution |
In our final example, we are going to find the sum of a sequence when we aren't initially given the value of the nth term (or the last term in the sequence we are summing). The only difference between this example and the previous example is that we will need to calculate the value of the nth term ourselves. This isn't too difficult, because we have already learned the formula for that as well.
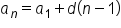
Recall that:
 : the value of the nth term
: the value of the nth term : the value of the 1st term
: the value of the 1st term : the common difference
: the common difference : the term
: the termEXAMPLE
Find the sum of the first 100 terms of the following sequence:
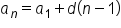
|
Substitute  , ,  , , 
|

|
Subtract 1 from 100 |

|
Multiply 7 and 99 |

|
Add 4 and 693 |

|
This is the value of the 100th term |

|
Substitute  , ,  , , 
|

|
Add 4 and 697 |

|
Divide 100 by 2 |

|
Multiply 50 and 701 |

|
Our solution |
 is the first term, and
is the first term, and  is the last or the nth term that you want to sum. When finding the sum when an is given, we just plug in the first and nth term into the formula. When finding the sum when an is not given, we don't have the nth term. We can determine
is the last or the nth term that you want to sum. When finding the sum when an is given, we just plug in the first and nth term into the formula. When finding the sum when an is not given, we don't have the nth term. We can determine  by using the formula for an arithmetic sequence, where
by using the formula for an arithmetic sequence, where  is the first term, d is the common difference, and n is the number of terms that you are summing.
is the first term, d is the common difference, and n is the number of terms that you are summing.
Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License