Five Number Summary and Boxplots

1. Five Number Summary

The five number summary takes larger data sets and makes them more manageable and easier to understand. By breaking down large data sets from many numbers to just five, this method can help to summarize the center and variability.

The five number summary consists of five parts:

• Minimum
• Q1
• Median
• Q3
• Maximum

term to know

Five Number Summary

A brief overview of a data set consisting of the minimum, the first quartile, the median, the third quartile, and the maximum.

2. Obtaining the Five Numbers

Two of the numbers in the five number summary are the smallest and largest--the minimum and the maximum.

EXAMPLE

Suppose you have a list of the heights of the Chicago Bulls basketball team:

Height of Chicago Bulls Players
Omer Asik	84
Carlos Boozer	81
Ronnie Brewer	79
Jimmy Butler	79
Luol Deng	81
Taj Gibson	81
Richard Hamilton	79
Mike James	74
Kyle Korver	79
John Lucas III	71
Joakim Noah	83
Derrick Rose	75
Brian Scalabrine	81
Marquis Teague	74
C.J. Watson	74

The median measures the center of a data set; it's the middle of an ordered set of data. Currently, this is alphabetical by the last name, so it needs to be rearranged from least to greatest height order. We can then see that the middle number, 79, is the median.

Dividing at that point, you are left with two groups: a low group and a high group. Next, take the median of each of those data sets. Now you have 74 in the low group, 81 in the high group, and 79 in the middle.

In this data set, 74 is the first quartile, 79 is the second quartile or the median, and 81 is the third quartile.

Now, the five number summary consists of the following five numbers.

• Minimum
• First quartile (Q1)
• Second Quartile/Median (Q2)
• Third quartile (Q3)
• Maximum.

You'll notice that:

• 25% of the data falls at or below the first quartile
• 50% falls at or below the median
• 75% falls at or below the third quartile
• All the data falls at or below the maximum

Also, you can see where a concentration of data values lie within the data set. For instance, there are more data values in a narrower range. There are the same amount of data values between 79 and 81, as there are between 74 and 79. Although it's the same number of data values, the range of the 79 to 81 band is narrower than the 74 to 79 band. Therefore, you can tell the data are more clustered together in the 79 to 81 band versus the 74 to 79 band.

terms to know

Quartiles

The values that divide the data set into four equal partitions.

First/Lower Quartile

The number at which approximately 25% of the data set falls at or below that value.

Second Quartile/Middle Quartile/Median

The number at which approximately 50% of the data set falls at or below that value.

Third/Upper Quartile

The number at which approximately 75% of the data set falls at or below that value.

3. Box-and-Whisker Plots/Boxplots

Boxplots are also sometimes called box-and-whisker plots. A boxplot is a way to graphically display the five number summary for a data set. It is composed of a box, which contains the middle 50% of the values, and whiskers, which extend out to the maximum and minimum values.

To create a boxplot, following the simple steps below:

step by step

Step 1: Draw an axis. It can be horizontal or vertical.
Step 2: Scale the axis with equal increments.
Step 3: Make a mark to identify the five numbers from the five number summary.
Step 4: Draw a box from the first quartile to the third quartile. Draw a whisker from Q1 to the minimum and from Q3 to the maximum.

EXAMPLE

Refer to the chart above of the heights of the Chicago Bulls basketball team. Recall that the five number summary consists of:

• Minimum: 71
• Q1: 74
• Median: 79
• Q3: 81
• Maximum: 84

So, how do you put this information into a boxplot?

step by step

Step 1: Draw an axis. It can be horizontal or vertical.
Step 2: Scale the axis with equal increments. Here, the graph includes the lowest number, 71, to the tallest number, 84.

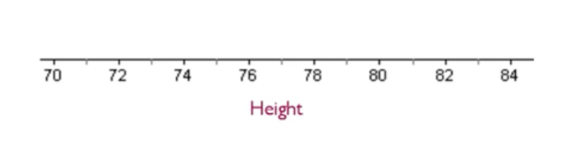
Step 3: Make a mark to identify the five numbers from the five number summary: 71, 74, 79, 81, and 84.

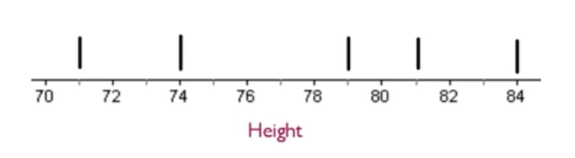
Step 4: Draw a box from the first quartile to the third quartile. The box shows where the middle 50% of the data lies. Then, about 25% percent of the data falls in the "whisker" to the left side, and about 25% of the data falls in a "whisker" to the right side. This is why it's sometimes called a box-and-whisker plot.

term to know

Boxplot/Box-and-Whisker Plot

A graphical distribution of the five number summary. The "box" in the middle contains the middle 50% of the values, and the "whiskers" extend out to the maximum and minimum values from the quartiles.

4. Using Boxplots: Comparing Two or More Distributions

You can use boxplots to compare two distributions. For instance, if you were talking about the heights of girls versus boys, you might be able to compare them by saying the spread, or the variation, with the girls, is much less than the variation with boys.

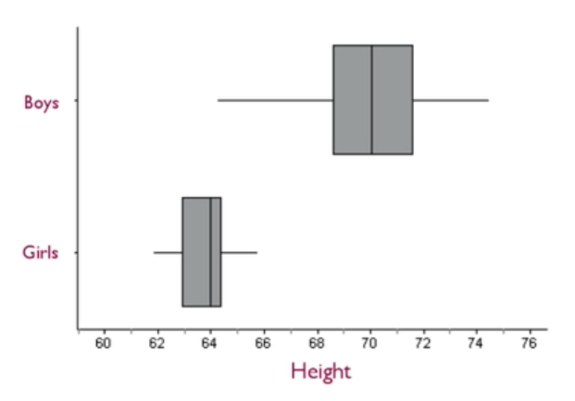
You can see this variation not only in the width of the boxes but also in the total width from the minimum to the maximum in each of these two data sets. Therefore, you can use boxplots as sort of a summary distribution for the boys and the girls.