Forms of Linear Equations

1. Slope-Intercept Form

Linear equations can be written in several forms. Each form has its pros and cons as to why we would want to express the equation in such a format. This is because certain information about the line and the linear relationship it represents can be easily identified just by looking at its equation. The first form is slope-intercept form.

The equation of a line written in slope-intercept form is:

formula to know

Slope-Intercept Form of a Line

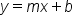
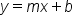
We refer to this form as slope-intercept form, because the equation readily gives us information about the line's slope, and its y-intercept. The variable represents slope, and the variable 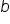represents the y-coordinate of the y-intercept (remember that the x-coordinate of a y-intercept is always zero).

EXAMPLE

Identify the slope and y-intercept of the equation .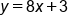

• : The line has a slope of 8
• : The y-intercept is at (0, 3)

2. Point-Slope Form

Linear equations can also come written in Point-Slope form. Point-Slope form, as the name suggests, provides information about the line's slope and a point on the line. Point-Slope form is as follows:

formula to know

Point-Slope Form of a Line

Once again, we can easily identify the line's slope by the variable m. Here, we also have and 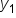. These represent the x-coordinate and y-coordinate of a point on a line.

EXAMPLE

Identify the slope and y-intercept of the equation .

• : The line has a slope of 3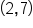
• : The point (2, 7) is a point on the line.

hint

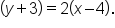Be careful with equations such as Our general form has minus signs with our x's and y's, if we see a plus sign in a specific equation, that coordinate actually is a negative value. In this example, (4, -3) is the point on the line.

EXAMPLE

Identify the slope and y-intercept of the equation .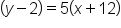

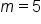• : The line has a slope of 5
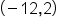• : The point (-12, 2) is a point on the line.

3. Standard Form

A final form we will discuss today is called Standard Form. Unlike slope-intercept form, or point-slope form, we cannot readily identify the slope, y-intercept, or point on a line simply by looking at the equation in standard form. However, the benefit of standard form is that any linear equation can be written in standard form, whereas not every line can be written in slope-intercept or point-slope forms. Think about a vertical line. It is an undefined slope. Both slope-intercept and point-slope forms rely on a defined slope to generate their equation. A vertical line, however, can be written in standard form, because a slope is not needed to write its equation.

formula to know

Standard Form of a Line

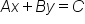
Here are some examples of equations written in standard form:

• A, B, and C should be integers. If any of them are not, the entire equation should be multiplied so that they are, if possible.
• A should be a positive integer. B and C are allowed to be negative, but if A is negative, the equation should be multiplied by -1 so as to make A positive.
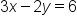
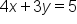
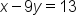
• Wherever possible, A, B, and C should be relatively prime. This means that they should have no common factors other than 1, if possible. For example, mathematicians prefer to be written as 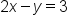, canceling out the common factor of 2 in both Ax, By, and C.