Table of Contents |
It’s often useful to graph equations in order to visually represent the relationship between variables. To graph a line, you only need to find at least two points on the line. There are several ways to graph a line:
The slope-intercept form of an equation can be used to more easily graph a line. Equations in slope-intercept form look like this:
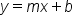
This formula is called "slope-intercept form" because you can easily identify the slope and the y-intercept of the line. In this equation, the variable m represents the slope of the line.

The variable b in the equation represents the y-intercept of the line. The coordinate point of the y-intercept is (0, b) and the y-intercept is the location on a graph where a line or a curve intersects the y-axis.

You can visually identify slope and a y-intercept on a graph.
EXAMPLE
Consider the equation of this graph:



You can use the variables in an equation in slope-intercept form to actually graph the equation.
EXAMPLE
 .
.
Source: This work is adapted from Sophia author Colleen Atakpu.