Table of Contents |
Previously we learned to solve inequalities with only one variable:
EXAMPLE
Solve the inequality , graph, and write in interval notation.
, graph, and write in interval notation.

|
Divide both sides by -2 |

|
Divide by a negative - flip symbol! |

|
Graph, starting at -3, going down with a closed circle for less than or equal to |

| |

|
Interval Notation |
But what about inequalities that contain two variables, such as  ? In particular, we will look at linear inequalities in two variables which are very similar to the linear equations we have seen in this unit.
? In particular, we will look at linear inequalities in two variables which are very similar to the linear equations we have seen in this unit.
When graphing a linear inequality, we generally follow these steps:
 using either a solid or dashed line
using either a solid or dashed lineLet's break down each step further:
1. Analyze the inequality symbol to determine a solid or dashed line: First, we need to decide if the graph of the linear inequality will have a solid or a dashed line. Solid lines indicate that the exact value of y is included in the solution to the inequality. We use solid lines when the inequality symbol is non-strict, or includes "or equal to." These would be our inequality symbols ≤ and ≥.
On the other hand, we use dashed lines when the exact value of y is not allowed in our solution to the inequality. Dashed lines represent strict inequalities, which do not include "or equal to." These are the symbols < and >.
| Endpoint IS included in interval | Endpoint IS NOT included in interval |
|---|---|
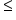 or or 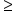
|
< or > |

|

|
2. Graph the equation of the line as y = using either a solid or dashed line: Once we have determined what kind of line to use when graphing the inequality, we need to actually graph it. To do so, we somewhat ignore the fact that we are dealing with an inequality, and simply graph the line as if it were  rather than with an inequality symbol. Just remember to use the appropriate line.
rather than with an inequality symbol. Just remember to use the appropriate line.
3. Determine a solution region to shade either above or below the line: We're not finished with the graph of our inequality yet. Next, we need to shade in half of the coordinate plane to represent the solution region. The solution region highlights all possible x- and y-coordinates that satisfy the inequality. When boundary lines are in the form  (with the variable y isolated on one side), it is simple enough to once again examine the inequality symbol to see which portion of the coordinate plane to shade.
(with the variable y isolated on one side), it is simple enough to once again examine the inequality symbol to see which portion of the coordinate plane to shade.
EXAMPLE
Graph the linear inequality .
.
| Step | Explanation | Graph |
|---|---|---|
| 1. Use solid or dashed line. | To start, we note that the inequality symbol is strict, thus we will use a dashed line. |

|
2. Graph the equation of the line as  . .
|
Next, we note the y-intercept of -5 and the positive slope of 2 to create the start of our graph. |

|
| 3. Shade above or below the line. |
Since our inequality is  , a less-than inequality, we know to shade everything below our dashed line. , a less-than inequality, we know to shade everything below our dashed line.
|

|
 is considered the boundary line, where coordinates on one side of the line are solutions, and coordinates on the other side of the line are non-solutions. The highlighted region is known as the solution region, as it shows all possible x- and y-values that satisfy the inequality.
is considered the boundary line, where coordinates on one side of the line are solutions, and coordinates on the other side of the line are non-solutions. The highlighted region is known as the solution region, as it shows all possible x- and y-values that satisfy the inequality.
While using the above method to determine which half of the coordinate plan to shade, there is a more mathematically sound method. This method will be particularly useful when graphing non-linear inequalities, where "above the line" and "below the line" aren't as clear cut.
A test point is any coordinate (x, y) that does not lie on the boundary line. We can think of it as being a representative for all other coordinates on that side of the boundary line. If our test point satisfies the inequality, it represents a solution, as do all the other points on that side. If our test point does not satisfy the inequality, then it represents a non-solution, and the other side of the boundary line should be shaded.
EXAMPLE
Consider the example from above. Suppose we have completed Step 2 and have drawn our boundary line. Now we need to determine which side to shade.

|
Plug in the point (0, 0) into the inequality |

|
Multiply 2 and 0 |

|
Subtract 5 from 0 |

|
 is a false statement, meaning (0, 0) is not in the solution region is a false statement, meaning (0, 0) is not in the solution region
|

Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License