Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Graphing Parabolas

Author: Sophia
PDF Version

what's covered
In this lesson, you will learn how to determine the graph of a quadratic equation in standard form. Specifically, this lesson will cover:

Table of Contents

1. Graphing Equations in Standard Form

The equation that is provided to you will determine what information you need to analyze in order to create a graph of a parabola. Quadratic equations in both standard form and vertex form provide the necessary information to plot the vertex of the parabola, although in different ways.

Recall the formula for standard form of a quadratic equation:

formula to know
Standard Form to Vertex Form
y equals a x squared plus b x plus c

The coefficient in front of the x-squared term, a comma will tell you if the parabola opens upwards or downward.

  • If a is a positive value, then the parabola opens upwards, and will have a U-shape to it. This means that the vertex is a minimum point.
  • If a is negative, then the parabola will open downward, with an upside down U-shape to it. This means that the vertex is a maximum point to the parabola.
The vertex lies on the parabola's axis of symmetry, which is a line of reflection that cuts the parabola in half. This helps us graph parabolas because if we know this axis of symmetry, we can plot a few points on one side of the parabola, and then just reflect them over to find points on the other side. With only a few points plotted on each side of the axis of symmetry, we can draw the general shape of the parabola.

To find the axis of symmetry with equations in standard form, we can actually use the formula for the x-coordinate of the vertex:

formula to know
x-Coordinate of Vertex
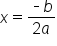
x equals fraction numerator short dash b over denominator 2 a end fraction

In the above formula, a and b come from the coefficients of the x-squared and x-terms in standard form.

EXAMPLE

Find the axis of symmetry and vertex for the equation y equals short dash x squared minus 2 x plus 3.

Since the equation is in standard form, we can identify the values of a comma b, and c as a equals short dash 1 comma space b equals short dash 2 comma space c equals 3. Now, we can plug the values of a and b into the formula for the x-coordinate of the vertex.

x equals short dash fraction numerator b over denominator 2 a end fraction Plug the values a equals short dash 1 and b equals short dash 2 into the formula for the x-coordinate of the vertex
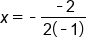
x equals short dash fraction numerator short dash 2 over denominator 2 open parentheses short dash 1 close parentheses end fraction Multiply 2 and -1
x equals short dash fraction numerator short dash 2 over denominator short dash 2 end fraction Divide -2 by -2
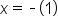
x equals short dash open parentheses 1 close parentheses Simplify
x equals short dash 1 x-coordinate of the vertex

The solution x equals short dash 1 actually gives us two pieces of information: the x-coordinate of the vertex AND the equation of the axis of symmetry.

In order to find the y-coordinate of the vertex, we can plug -1 into the original equation, and solve for y. Then we will be able to plot the vertex on the graph:

y equals short dash x squared minus 2 x plus 3 Using the original quadratic equation, plug in -1 for x
y equals short dash open parentheses short dash 1 close parentheses squared minus 2 open parentheses short dash 1 close parentheses plus 3 Evaluate
y equals short dash 1 plus 2 plus 3 Simplify
y equals 4 y-coordinate of the vertex

The vertex to the parabola is at the point (-1, 4) with a line of symmetry at x equals short dash 1. Let's sketch the graph so far:



Now, we just need to figure out a few points to be plotted on one side of the parabola. Then we'll be able to reflect about the line of symmetry to complete our graph. Let's choose some x-values on the right side of the axis of symmetry.

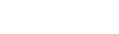
x bold italic y bold equals bold short dash bold italic x to the power of bold 2 bold minus bold 2 bold italic x bold plus bold 3 (x, y)
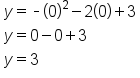
0 table attributes columnalign left end attributes row cell y equals short dash open parentheses 0 close parentheses squared minus 2 open parentheses 0 close parentheses plus 3 end cell row cell y equals 0 minus 0 plus 3 end cell row cell y equals 3 end cell end table (0, 3)
1 table attributes columnalign left end attributes row cell y equals short dash open parentheses 1 close parentheses squared minus 2 open parentheses 1 close parentheses plus 3 end cell row cell y equals short dash open parentheses 1 close parentheses minus 2 plus 3 end cell row cell y equals 0 end cell end table (1, 0)
2 table attributes columnalign left end attributes row cell y equals short dash open parentheses 2 close parentheses squared minus 2 open parentheses 2 close parentheses plus 3 end cell row cell y equals short dash open parentheses 4 close parentheses minus 4 plus 3 end cell row cell y equals short dash 5 end cell end table (2, -5)

Here is the sketch of the graph with these points plotted, as well as point reflected about the axis of symmetry:

2. Graphing Equations in Vertex Form

When equations are provided in vertex form, we still want to locate the parabola's vertex, plot a few points on one side of the axis of symmetry, and reflect them to plot a more complete graph. However, finding the coordinates of the vertex using this equation is much easier. The only tricky thing is to keep the sign in mind.

Recall the formula for vertex form of a quadratic equation:

formula to know
Vertex Form of a Quadratic Equation
y equals a left parenthesis x minus h right parenthesis squared plus k

The variables h and k describe the x- and y-coordinates of the vertex: (h, k)

hint
Notice that generally, there is a minus sign between x and h. So if the equation has a plus sign between x and h, the value of h is negative, rather than positive. This can be counterintuitive, so keep this in mind.

EXAMPLE

Find the axis of symmetry and vertex for the equation y space equals space left parenthesis x plus 2 right parenthesis squared plus 1.

We can identify the vertex right away from equations in this form. The vertex of this parabola is located at the point (-2, 1). Remember, h has a value of -2 since the equation contains open parentheses x plus 2 close parentheses. We take the sign of k with us, so we know that the y-coordinate remains positive.

We can now graph the parabola's vertex, along with its axis of symmetry:



Similarly, we will choose a few x-values on one side of the axis of symmetry, and find their associated y-values. We can then plot points and reflect them about the axis of symmetry to create a nice sketch of the parabola:

x bold italic y bold equals open parentheses bold x bold plus bold 2 close parentheses to the power of bold 2 bold plus bold 1 (x, y)
-1 table attributes columnalign left end attributes row cell table attributes columnalign left end attributes row cell y equals open parentheses short dash 1 plus 2 close parentheses squared plus 1 end cell row cell y equals open parentheses 1 close parentheses squared plus 1 end cell row cell y equals 1 plus 1 end cell end table end cell row cell y equals 2 end cell end table (-1, 2)
0 table attributes columnalign left end attributes row cell y equals open parentheses 0 plus 2 close parentheses squared plus 1 end cell row cell y equals 2 squared plus 1 end cell row cell y equals 4 plus 1 end cell row cell y equals 5 end cell end table (0, 5)
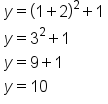
1 table attributes columnalign left end attributes row cell y equals open parentheses 1 plus 2 close parentheses squared plus 1 end cell row cell y equals 3 squared plus 1 end cell row cell y equals 9 plus 1 end cell row cell y equals 10 end cell end table (1, 10)

summary
When graphing equations in standard form, the constant c is the y-intercept of the parabola. The vertex of a parabola can be calculated using the a and b coefficients in the standard form. When graphing equations in vertex form, the vertex can be found by identifying the values for h and k in the vertex form. The vertex of a parabola lies on the parabola's axis of symmetry. As such, points plotted on one side of the parabola can be reflected across the axis to represent more points on the parabola.

Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License

Formulas to Know
Standard Form to Vertex Form

y equals a x squared plus b x plus c

Vertex Form of a Quadratic Equation

y equals a open parentheses x minus h close parentheses squared plus k

X-Coordinate of Vertex

x equals fraction numerator short dash b over denominator 2 a end fraction

© 2024 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.