Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Graphing Quadratic Inequalities

Author: Sophia
PDF Version

what's covered
In this lesson, you will learn how to determine the graph of a quadratic inequality. Specifically, this lesson will cover:

Table of Contents

1. Graphing a Parabola

More than likely, you'll be given a quadratic equation or inequality in standard form 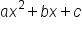a x squared plus b x plus c. To graph this, it is helpful to find the vertex to the parabola, and then plot some points on one side of the vertex. Since the vertex lies on the axis of symmetry, we can simply reflect the already plotted points across this line, to create a more complete sketch of the parabola.

To find the vertex and/or axis of symmetry when working in standard form, we use the following formula, where a and b come from the coefficients of the x-squared and x-terms in standard form:

formula to know
x-Coordinate of Vertex
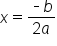
x equals fraction numerator short dash b over denominator 2 a end fraction

This formula is also the equation to the vertical line which is the axis of symmetry (for vertical parabolas). This also represents the x-coordinate of the vertex. To find the y-coordinate, simply use the calculated value of x in the original equation, and solve for y.

2. Graphing an Inequality

Graphing inequalities is similar to graphing equations, but there are some important differences. First, there is a difference between using a solid line and a dashed line to draw the curve. If the inequality symbol is strict ( < or >) we always use a dashed line to show that we are not including exact values on the boundary line. If the inequality symbol is non-strict ( ≤ or ≥ ) we always use a solid line to show that we are including exact values on the boundary line.

Not only do we need to be careful about what type of line to use when drawing the graph, but we also need to highlight a solution region. The highlighted solution region represents the set of all (x, y) coordinates that satisfy the inequality. To decide which inequality region to highlight, we use a test point. This test point can be anywhere on the coordinate plane, so long as it isn't on the boundary line (because that would not help us at all). We take the x- and y- values from this test point and plug it into our inequality. If the statement is true, the half-plane that the test point lies within is the solution region, and gets highlighted. If not, the other half-plane gets highlighted.

3. Graphing a Quadratic Inequality

Let's apply what we know about graphing parabolas and graphing inequalities to graph a quadratic inequality.

EXAMPLE

Graph the inequality y greater or equal than x squared minus 2 x plus 2.

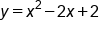The first thing we need to do is graph the boundary line, y equals x squared minus 2 x plus 2. We will use a solid line to graph the parabola because our inequality symbol is non-strict. To graph the boundary line, we need to find the vertex, plot a couple of points, and then reflect them across the axis of symmetry:

To plot the vertex, we first identify the values of a and b in the standard form equation and then substitute those values into the formula for the x-coordinate of the vertex.

x equals short dash fraction numerator b over denominator 2 a end fraction Plug in the values a equals 1 and b equals short dash 2
x equals short dash fraction numerator short dash 2 over denominator 2 open parentheses 1 close parentheses end fraction Evaluate
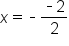
x equals short dash fraction numerator short dash 2 over denominator 2 end fraction Divide
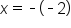
x equals short dash open parentheses short dash 2 close parentheses Simplify
x equals 1 x-coordinate of the vertex

We use x equals 1 to draw the axis of symmetry. We can also use this to find the y-coordinate of the vertex:

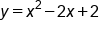
y equals x squared minus 2 x plus 2 Substitute 1 in for x
y equals open parentheses 1 close parentheses squared minus 2 open parentheses 1 close parentheses plus 2 Evaluate
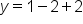
y equals 1 minus 2 plus 2 Simplify
y equals 1 y-coordinate of vertex

The vertex is located at the point (1, 1). Next, we plot a few points on one side of the vertex, and reflect them across the axis of symmetry to sketch the boundary line:

x bold italic y bold equals bold italic x to the power of bold 2 bold minus bold 2 bold italic x bold plus bold 2 (x, y)
2 table attributes columnalign left end attributes row cell y equals 2 squared minus 2 open parentheses 2 close parentheses plus 2 end cell row cell y equals 4 minus 4 plus 2 end cell row cell y equals 2 end cell end table (2, 2)
3 table attributes columnalign left end attributes row cell y equals 3 squared minus 2 open parentheses 3 close parentheses plus 2 end cell row cell y equals 9 minus 6 plus 2 end cell row cell y equals 5 end cell end table (3, 5)
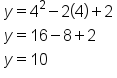
4 table attributes columnalign left end attributes row cell y equals 4 squared minus 2 open parentheses 4 close parentheses plus 2 end cell row cell y equals 16 minus 8 plus 2 end cell row cell y equals 10 end cell end table (4, 10)



The final step is to choose any test point (not on the boundary line) and plug the x- and y-values into the inequality. Remember, a true statement means the point lies within the solution region (and that half-plane should be shaded). Otherwise, the other half-plane gets shaded.

Use the test point (0, 0) if you can. This is because it is easy to multiply by zero and add zero to quantities. It is always recommended to make calculations simpler!

y greater or equal than x squared minus 2 x plus 2 Plug in the point (0, 0) into the original inequality
0 greater or equal than open parentheses 0 close parentheses squared minus 2 open parentheses 0 close parentheses plus 2 Evaluate
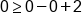
0 greater or equal than 0 minus 0 plus 2 Simplify
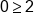
0 greater or equal than 2 False statement

Since the point (0, 0) yields a false statement, we highlight the other region of the coordinate plane as our solution region (we do not highlight the region that includes the origin (0, 0) in this case):

summary
To graph a quadratic inequality, we graph the parabola as we do with equations, but use either a dotted or a solid line, depending on the inequality. When graphing an inequality, the inequality symbols less than and greater than indicate using dotted or dashed lines, and inequality symbols less than or equal to or greater than or equal to indicate using solid lines. When graphing a quadratic inequality, the solution to the inequality can be represented by shading a portion of the plane. If a test point yields a true inequality statement, then the region the point lies in is shaded. If a test point yields a false inequality statement, then the other portion of the plane is shaded as the solution region.

Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License

Formulas to Know
X-Coordinate of Vertex

x equals fraction numerator short dash b over denominator 2 a end fraction

© 2024 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.