Histograms

1. Histograms

Histograms are a type of distribution for quantitative data. When you have a quantitative data set, often the values are spread out over a large range of values.

Suppose there's an elementary school class in Muncie, Indiana that chooses to keep track of the high temperature on each of the 180 school days. In Indiana, the temperature can get low in the winter, down to zero degrees Fahrenheit, and maybe near 90℉ at the beginning or the end of the school year.

To understand the overall trend of the data, you might not be interested in every single individual temperature. Instead, you might be more interested in how many days were in the 20℉'s--that is, days that the temperature was in the range of 20℉ up to 29.999℉, or in the 30s℉, 40s℉, etc.

The idea that we can break those temperatures that occur over a wide range into more manageable intervals and categorize them that way is called binning. Binning allows us to make a frequency table out of those categories.

Using the bin width of 10, the Muncie School District recorded the temperature on every day, then categorized them by whether they were in 0℉'s, 10℉'s, 20℉'s, 30℉'s, 40℉'s, 50℉'s, 60℉'s, 70℉'s, 80℉'s, or 90℉'s, and created the following frequency table.

This means there was one day out of the year that it hit the 90℉'s, seven days were in the 80℉'s, etc. Now we can create a histogram.

A histogram is somewhat similar to a bar graph in that, on the horizontal axis, you’re going to display the temperatures, which are our categories now. The only difference is these categories are numbers. Our bins go from 0 to 10, 10 to 20, 20 to 30, 30 to 40, etc. so it makes sense that we would put 0 as being first, and ten as being second, and 20 as being third. The frequencies, just like a bar graph, will go up the vertical axis.

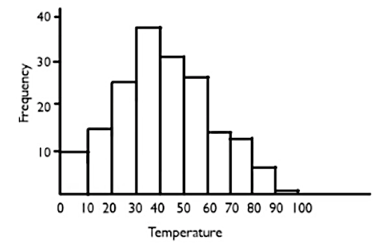
As you can see from this histogram, the first bin goes from 0 degrees to 10 degrees, and ten days fall into that category. The second bin goes from 10 degrees to 20 degrees, and because there are 16 days there, that bar goes all the way up to 16. Every bar reflects the data from the table.

terms to know

Histogram

A distribution of data that shows the frequency of different ranges of values. Each frequency is the height of a bar.

Binning

The method of deciding what widths of categories should be used on a histogram.

2. Binning

The way we choose to bin data can change the look, and at times, the shape of the histogram.

In the original histogram, data was classified by 10's. But what if you chose to classify it by 5-degree intervals instead? Instead of going 0℉ to 10℉, what if we split up the values between 0℉ to 4℉ and 5℉ to 9℉, 10℉ to 14℉, and 15℉ to 19℉, etc.? In that case, the bins might look different.

Reviewing the frequency table, there are ten days in the range between 0℉ and 10℉. Suppose there were four days between 0℉ and 4℉, and six days were between 5℉ and 9℉. Therefore, we took one bin and split it into two bins. If you do that with every one of your bins, you end up with twice as many bins and twice as many bars on your histogram.

In this new histogram, notice the frequencies. The bars are not as tall as they were before, but they still provide the same overall shape. However, there are not very many bars overall. There's a lot of data in one part of the graph and not a lot in the other parts. You'll note that in the 90 to 95 bin, there's no bar. The reason for this is that when we broke up that bar, the one data value that was in the 90's was actually in the 95 to 99 range. When there's no data in a particular bin, there's not going to be any bar that extends up from the x-axis.

big idea

The binning process is important. Problems can arise if you make the bins too narrow. In the previous examples, there were bins of width 10 degrees and bins of width 5 degrees. You could have decided on bins with width 1 or 2 degrees, but perhaps you wouldn't have gotten the same overall shape of the distribution.

There are two main problems you may have with binning:

• The pancake effect: Bins that are too narrow can create the pancake effect, displaying too many bins with almost nothing in them. You don't really get to see the overall shape of the data. Suppose that our bins go from 0 degrees to 2 degrees, 2 degrees to 4 degrees, etc. If we continued to do this with all of our data, we would end up with much more bins, but hardly any data in each bin.

• The skyscraper effect: Bins that are too wide can create the skyscraper effect. Suppose that your bins go from 0 degrees to 50 degrees and then 50 degrees to 100 degrees. If you have too few bins and lots of data in them, you don't get an accurate sense of what the shape of the distribution looks like. You know that most of the data is in one bin and not the other, but you don't know where in the first bin that data is. The classes and bins were too wide, so you don't get an overall understanding of the distribution.

3. Histograms and Bar Graphs

You might confuse a bar graph with a histogram from time to time. However, there are two key differences between the two kinds of graphs.