First, please create an account

Already have a Sophia account?

Imaginary and Complex Numbers

Author: Sophia

what's covered

In this lesson, you will learn how to determine the value of a power of i. Specifically, this lesson will cover:

1. Complex Numbers
2. The Complex Plane
3. Powers of i

1. Complex Numbers

A complex number is a number that contains a real part and an imaginary part, such as 6 minus 5 i . In mathematics, we deal with real numbers all the time. These are numbers that we can place on the number line, such as integers, decimals and fractions, and rational and irrational numbers. An imaginary number is not real, and contains the imaginary unit i, which is square root of negative 1 end root . This is non-real because every real number squared is non-negative. So when a negative number is underneath a square root, there is no real number that it evaluates to.

In general, we write complex numbers in the form a plus b i . is the real number component to the complex number, and b i is the imaginary number component to the complex number. Complex numbers represent a larger set of numbers than real numbers do, because the complex number system includes real numbers, and also includes the set of all imaginary numbers as well.

term to know

Complex Number

A number in the form a plus b i

, containing a real part,

, and an imaginary part, bi, where i is the imaginary unit, square root of short dash 1 end root

2. The Complex Plane

We can represent complex numbers on what is called the complex plane. It is similar to the coordinate plane we use for graphing, but instead of x- and y-axes, we have a real axis and an imaginary axis. This is shown below:

We can plot complex numbers on the complex plane following a very similar process for plotting coordinate points (x, y) on the coordinate plane.

EXAMPLE

Plot the following points on the complex plane:

Notice that there are positive and negative sides to the complex plane, just as there are positive and negative sides to the coordinate plane. Also, note the numbers negative 2 i

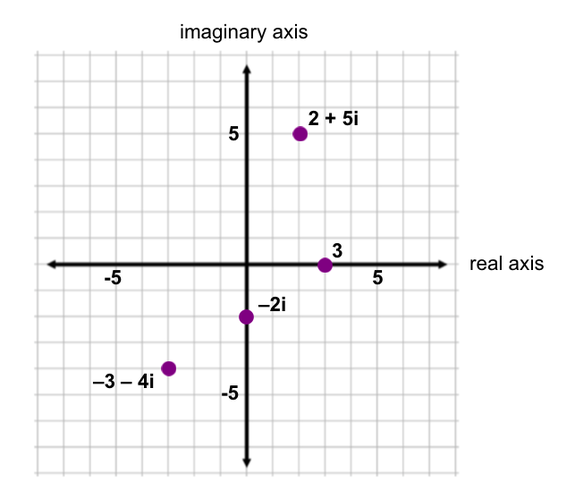
and

. These numbers lie on one of the axes of the plane because they are either purely imaginary (having no real component) or purely real (having no imaginary component).

3. Powers of i

There is an interesting pattern with the powers of the imaginary unit, i. The pattern is cyclical, which means that it repeats in cycles. Let's examine the first four powers of i:

Power of i	Calculation	Result

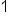
At this point, as we continue to increase the exponent by one, the powers of i repeat this cycle: i comma space short dash 1 comma space short dash i comma space 1

formula to know

Imaginary Number

table attributes columnalign left end attributes row cell i equals square root of short dash 1 end root end cell row cell i squared equals short dash 1 end cell end table

summary

Complex numbers consist of a real part and an imaginary part. Looking at the complex plane, complex numbers encompass a larger set of numbers than real numbers, because they include imaginary numbers. The square root of negative 1 is imaginary, because no real number squared results in negative number. When looking at increasing powers of i, the solutions follow a pattern of i, negative 1, negative i, and 1, continuously.

Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License

Terms to Know

Complex Number: A number in the form $a plus b i$ , containing a real part, $a$ , and an imaginary part, bi, where i is the imaginary unit, .

Formulas to Know

Imaginary Number: $i equals square root of short dash 1 end root i squared equals short dash 1$

First, please create an account

Imaginary and Complex Numbers

Table of Contents

1. Complex Numbers

2. The Complex Plane

3. Powers of i