Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Introduction to Absolute Value

Author: Sophia
PDF Version

what's covered
In this lesson, you will learn how to determine the result of an expression with absolute value. Specifically, this lesson will cover:

Table of Contents

1. Introduction to Absolute Value

The absolute value of a number is its distance from zero on the number line. To illustrate this, let's take a look at a number on the number line, and identify its distance from zero:

As we can see in the number line above, the number 4 is 4 units away from zero. This means that the absolute value of 4 is 4. This seems easy, and with positive numbers, it is very straightforward. But what about -4? The magnitude of the number is the same (the actual number we see, ignoring if it's positive or negative), but it is on the opposite side of 0 on the number line, as shown below:

We see that -4 is also 4 units away from 0 on the number line. This means that the absolute value of -4 is 4. Notice that with both 4 and -4, the absolute value is non-negative.

big idea
When taking the absolute value of a number, it is always non-negative. A simple way to think about evaluating the absolute value of a number is to rewrite the number without regard to its sign (do not write positive or negative, just the number).

term to know
Absolute Value
The distance between a number and zero on the number line; it is always non-negative.

2. Adding and Subtracting with Absolute Value

Now that we have an understanding of the absolute value of a number, let's use absolute value in addition and subtraction problems. The important thing here is to evaluate the absolute value first, and then perform the addition or subtraction.

EXAMPLE

open vertical bar 3 close vertical bar plus open vertical bar short dash 7 close vertical bar Evaluate open vertical bar 3 close vertical bar as 3
3 plus open vertical bar short dash 7 close vertical bar Evaluate open vertical bar short dash 7 close vertical bar as 7
3 plus 7 Add 3 and 7
10 Our Solution

EXAMPLE

open vertical bar short dash 4 close vertical bar minus open vertical bar 8 close vertical bar Evaluate open vertical bar short dash 4 close vertical bar as 4
4 minus open vertical bar 8 close vertical bar Evaluate open vertical bar 8 close vertical bar as 8
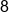
4 minus 8 Subtract 8 from 4
short dash 4 Our Solution

If there are multiple numbers and operations within absolute value bars, we must evaluate the expression inside before taking any absolute value. This is because absolute value bars also act as grouping symbols, and must be evaluated first according to the order of operations.

EXAMPLE

open vertical bar 4 plus short dash 3 minus 2 close vertical bar Add short dash 3 to 4
open vertical bar 1 minus 2 close vertical bar Subtract 2 from 1
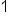
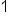
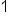
open vertical bar short dash 1 close vertical bar Evaluate open vertical bar short dash 1 close vertical bar as 1
1 Our Solution

3. Multiplying and Dividing with Absolute Value

There are a couple of special properties with absolute value when multiplying and dividing two numbers. Let's take a look at multiplication first:

EXAMPLE

open vertical bar 7 times short dash 3 close vertical bar Multiply 7 by short dash 3
open vertical bar short dash 21 close vertical bar Evaluate open vertical bar short dash 21 close vertical bar as 21
21 Our Solution

Now let's take a look at another way to approach the same problem:

open vertical bar 7 times short dash 3 close vertical bar Write as two absolute values
open vertical bar 7 close vertical bar times open vertical bar short dash 3 close vertical bar Evaluate open vertical bar 7 close vertical bar as 7
7 times open vertical bar short dash 3 close vertical bar Evaluate open vertical bar short dash 3 close vertical bar as 3
7 times 3 Multiply 7 by 3
21 Our Solution

big idea
With products, we can say that vertical line a times b vertical line equals open vertical bar a close vertical bar times open vertical bar b close vertical bar.

Next, let's see if the same property holds true with division:

EXAMPLE

open vertical bar short dash 18 divided by 2 close vertical bar Divide short dash 18 by 2
open vertical bar short dash 9 close vertical bar Evaluate open vertical bar short dash 9 close vertical bar as 9
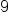
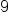
9 Our Solution

Do you think we will arrive at the same solution if we first rewrite the expression using two sets of absolute value bars?

open vertical bar short dash 18 divided by 2 close vertical bar Write as two absolute values
open vertical bar short dash 18 close vertical bar divided by open vertical bar 2 close vertical bar Evaluate open vertical bar short dash 18 close vertical bar as 18
18 divided by open vertical bar 2 close vertical bar Evaluate open vertical bar 2 close vertical bar as 2
18 divided by 2 Divide 18 by 2
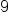
9 Our Solution

big idea
With quotients, we can say that open vertical bar a divided by b close vertical bar equals open vertical bar a close vertical bar divided by open vertical bar b close vertical bar.

hint
If you have a negative sign on the OUTSIDE of the absolute value, you will actually end up with a negative value. For instance:

table attributes columnalign left end attributes row cell short dash open vertical bar short dash 12 close vertical bar end cell row cell short dash open parentheses 12 close parentheses end cell row cell short dash 12 end cell end table

try it
Evaluate each expression below.
|-3| – |-5|
The absolute value of -3 is just 3 and the absolute value of -5 is just 5. The expression can be rewritten as:

table attributes columnalign left end attributes row cell vertical line short dash 3 vertical line minus vertical line short dash 5 vertical line end cell row cell 3 minus 5 space end cell row cell short dash 2 end cell end table
-|-7| + |4|
The absolute value of -7 is just 7 and the absolute value of 4 is just 4. Make sure you add back in the negative sign that is in front of the absolute value of -7. The expression can be rewritten as:

table attributes columnalign left end attributes row cell short dash open vertical bar short dash 7 close vertical bar plus 4 end cell row cell short dash open parentheses 7 close parentheses plus 4 end cell row cell short dash 7 plus 4 end cell row cell short dash 3 end cell end table
|-10| + |6|
The absolute value of -10 is just 10 and the absolute value of 6 is just 6. The expression can be rewritten as:

table attributes columnalign left end attributes row cell open vertical bar short dash 10 close vertical bar plus open vertical bar 6 close vertical bar end cell row cell 10 plus 6 end cell row 16 end table

summary
Absolute value is defined as the distance a number is away from 0 on a number line. Because it's a distance, it will always be a non-negative number. In other words, it will either be zero or a positive number. The absolute value sign acts as a grouping symbol. When you're adding and subtracting with absolute values, you would do things in the absolute value symbol first, just like parentheses. Finally, when multiplying and dividing absolute values, the product quotient properties of absolute value will allow us to simplify absolute value expressions.

Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License

Terms to Know
Absolute Value

The distance between a number and zero on the number line; it is always non-negative.

© 2024 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.