Table of Contents |
You may be familiar with equations that contain exponents. Take the polynomial equation 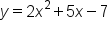 , for example. We see variables, and we see exponents. However, this is not an exponential equation. An exponential equation contains a variable exponent. This means that our variable x, for example, is part of the expression for the exponent, not a base number.
, for example. We see variables, and we see exponents. However, this is not an exponential equation. An exponential equation contains a variable exponent. This means that our variable x, for example, is part of the expression for the exponent, not a base number.
Generally, we say that an exponential equation is given by: 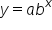
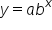
We have a base number, b, being raised to a variable exponent, x. We also have an a-value in front, which is a scalar multiplier to the exponential expression.
The domain (or values that x is allowed to take on) is all real numbers, from negative infinity to positive infinity. As such, there are some restrictions to the base. These are values for b that come into direct conflict with the all-real number domain:
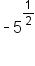 . This results in a non-real number (we can equivalently think of this as the square root of negative 5, or
. This results in a non-real number (we can equivalently think of this as the square root of negative 5, or 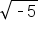 ).
). . This can be thought of as 1 divided by
. This can be thought of as 1 divided by 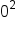 , or
, or  , which is division by zero and would result in a non-solution.
, which is division by zero and would result in a non-solution.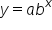 , the base b has to be greater than zero and cannot equal 1 (
, the base b has to be greater than zero and cannot equal 1 ( and
and 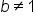 ).
).
Let's examine the pattern for exponential equations by looking at the relationship in a table.
EXAMPLE
Find the following values for the exponential equation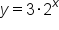 .
.
| x |
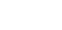
|
y |
|---|---|---|
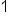
|
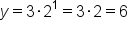
|
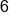
|

|
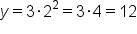
|

|

|
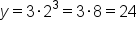
|

|
| x |
|
y |
|---|---|---|

|
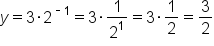
|
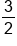
|

|

|

|

|
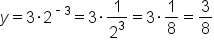
|

|
 and exponential equation have variables as the exponent, such as
and exponential equation have variables as the exponent, such as  is an equation involving a constant value raised to a variable power. The general form of an exponential equation is
is an equation involving a constant value raised to a variable power. The general form of an exponential equation is  times b to the x power.
times b to the x power.
Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License