Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Introduction to Parabolas

Author: Sophia
PDF Version

what's covered
In this lesson, you will learn how to determine the vertex and direction of opening of the parabola for a quadratic equation. Specifically, this lesson will cover:

Table of Contents

1. Upwards and Downwards Parabolas

When graphing quadratic relationships, we can describe the curve on the coordinate plane as a parabola. Parabolas open either upwards or downwards, creating a U-shape curve (in the case of an upward parabola) or an upside-down U-shape curve (in the case of a downwards parabola).

One form of a quadratic equation is y equals a x squared plus b x plus c, also known as standard form. The value of "a" dictates whether the parabola will open up or down. If a is a positive value, the parabola will open upwards. If a is a negative value, the parabola will open downwards.

2. Defining the Vertex of a Parabola

Given the shape of a parabola, there will always be either a low point or a high point to the curve. This point is referred to as the parabola's vertex. An interesting characteristic of the vertex is that it lies on an invisible line of symmetry. This means that parabolas are symmetrical - we can imagine reflecting one side of the parabola about the line of reflection, and it will match up with points on the other side. This line of reflection is known as the axis of symmetry to the parabola.

terms to know
Vertex (of a Parabola)
The minimum or maximum point of a parabola located on the axis of symmetry.
Axis of Symmetry
A line of reflection passing through the vertex of a parabola; in up and down parabolas, it is a vertical line.

3. Calculating the Vertex of a Parabola

There are a few ways to find the vertex of a parabola from its equation. When the equation of a parabola is given in standard form, we use the values a and b (the coefficients of the x-squared and x-terms) to calculate the x-coordinate of the vertex. This also describes the equation to the axis of symmetry. Here is the formula we use:

formula to know
x-Coordinate of Vertex
x equals negative fraction numerator b over denominator 2 a end fraction

Once we find the value for x, we plug that into the equation and find the associated y-value. This gives us the coordinates of the parabola's vertex.

EXAMPLE

Find the coordinates of the vertex for the quadratic equation y equals 2 x squared minus 4 x plus 5.

Since the equation is in standard form, we can identify the values of a comma b, and c as a equals 2 comma space b equals short dash 4 comma space c equals 5. Now, we can plug the values of a and b into the formula for the x-coordinate of the vertex.

x equals short dash fraction numerator b over denominator 2 a end fraction Plug the values a equals 2 and b equals short dash 4 into the formula for the x-coordinate of the vertex
x equals short dash fraction numerator short dash 4 over denominator 2 open parentheses 2 close parentheses end fraction Multiply 2 and 2
x equals short dash fraction numerator short dash 4 over denominator 4 end fraction Divide -4 by 4
x equals short dash open parentheses short dash 1 close parentheses Simplify
x equals 1 x-coordinate of the vertex

This also gives us the equation of the axis of symmetry. We could draw an imaginary line at x equals 1 that splits the parabola in half.

Now we can substitute 1 in for x in the original equation and solve for y to find the y-coordinate.

y equals 2 x squared minus 3 x plus 5 Using the original quadratic equation, plug in 1 for x
y equals 2 open parentheses 1 close parentheses squared minus 4 open parentheses 1 close parentheses plus 5 Evaluate
y equals 2 minus 4 plus 5 Simplify
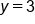
y equals 3 y-coordinate of the vertex

The vertex to y equals 2 x squared minus 4 x plus 5 is located at the point open parentheses 1 comma space 3 close parentheses.

4. Vertex Form of a Quadratic Equation

Finding the coordinates to a parabola's vertex is much easier if the equation is given in a different format, specifically the vertex form.

formula to know
Vertex Form of a Quadratic Equation
y equals a left parenthesis x minus h right parenthesis squared plus k

We don't call it the vertex form for nothing. The variables h and k represent the x- and y-coordinates of the vertex. So there are virtually no calculations needed in order to identify the vertex when it is in the form. The only tricky thing is to remember that in general, there is a minus sign between x and h, so we need to be mindful of the sign.

hint
It is easy to mistake the sign of h when finding the x-coordinate of the vertex. Because the general formula subtracts h from x, if we see a plus sign in the specific equation, our h value is actually negative.

EXAMPLE

Find the coordinates of the vertex for the quadratic equation y equals 2 open parentheses x plus 4 close parentheses squared plus 3.

y equals 2 open parentheses x plus 4 close parentheses squared plus 3 Identify h and k from the equation in vertex form
h equals short dash 4 comma space space space k equals 3 h is the value of the x-coordinate and k is the value of the y-coordinate of the vertex
left parenthesis short dash 4 comma space 3 right parenthesis Coordinates to the vertex

try it
Consider the following table of equations written in vertex form.
Equation in Vertex Form h k Coordinates of Vertex
y equals 3 open parentheses x minus 5 close parentheses squared plus 10
y equals short dash 7 open parentheses x plus 1 close parentheses squared plus 9
y equals 4 open parentheses x minus 8 close parentheses squared minus 2
y equals short dash 2 open parentheses x plus 6 close parentheses squared minus 15

Use the table to find the vertex coordinates of each equation.

Equation in Vertex Form h k Coordinates of Vertex
y equals 3 open parentheses x minus 5 close parentheses squared plus 10 5 10 (5, 10)
y equals short dash 7 open parentheses x plus 1 close parentheses squared plus 9 -1 9 (-1, 9)
y equals 4 open parentheses x minus 8 close parentheses squared minus 2 5 10 (8, -2)
y equals short dash 2 open parentheses x plus 6 close parentheses squared minus 15 5 10 (-6, -15) 















summary






A quadratic equation can either be an upwards or downwards parabola.  If the x-squared coefficient in a quadratic equation is positive, the graph of the equation parabola will be pointing up. If the x-squared coefficient is negative, the parabola will be pointing down. The vertex of a parabola is either the low point or the high point to the curve. The axis of symmetry acts as a line of reflection, so all points on the left of the parabola can be reflected across the axis of symmetry to represent all points to the right and vice versa.  With the vertex form of a quadratic equation, the variable h and k represent the x- and y-coordinates of the vertex.












Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License




















Terms to Know









Axis of Symmetry





A line of reflection passing through the vertex of a parabola; in up and down parabolas, it is a vertical line.





Vertex (of a Parabola)





The maximum or minimum point of a parabola located on the axis of symmetry.



















Formulas to Know









Vertex Form of a Quadratic Equation





y equals a left parenthesis x minus h right parenthesis squared plus k





X-Coordinate of Vertex





x equals fraction numerator negative b over denominator 2 a end fraction
































© 2024 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.