Introduction to Percents

1. What Is a Percent?

A percent or percentage is a number that relates a part to the whole, where the whole is always 100. The word percent literally means “per 100.” 50%, then, means 50 per every 100. The symbol % means percent in the percentage form of a number.

Percentages are used in daily life, like in the case of interest rates. An interest rate of 5% on a loan means that you paid five additional dollars for every $100 you borrowed. Percentages are also used to report data.

EXAMPLE

If 60% of people own their own home in a certain community, this means that 60 out of every 100 people own their own home.

term to know

Percentage

A number that relates a part to the whole

2. Percents as Fractions

You can think of percents as fractions as well. In the fraction form of a percent, 100 is the denominator.

EXAMPLE

If you have a coupon for 25% off, you would save $25 for every $100 you spend. 25% as a fraction would be 25 over 100, where 25 is the part and 100 is the whole.

EXAMPLE

Suppose you have a certain country that has been able to reduce their environmental emissions by 3% over the last two years. 3% as a fraction would be 3 over 100, where 3 is the part and 100 is the whole.

3. Converting Fractions and Decimals to Percents

How can you determine the percentage equivalent of a fraction? There are two general methods for converting a percent into a fraction.

The first method is to write an equivalent fraction with a denominator of 100. You can do this because you know that a percentage can be thought of as a portion of 100 or a certain number per 100.

EXAMPLE

Suppose you want to convert the fraction 2/5 into a percentage.

	Our Expression
	First, we want to write an equivalent fraction with 100 as the denominator.
	If we want the 5 in the denominator to be converted to 100, we will need to multiply it by 20. 5 times 20 equals 100. If we multiply the denominator by 20, we must also multiply the numerator by 20.
	20 times 2 equals 40.
	40/100 is the same at 40%.

Not all fractions can be easily written with a denominator of 100, so there is a second method that will easily work for all fractions. In this method, you convert your fraction into a percent by first converting the fraction to a decimal, and then converting the decimal to a percent.

EXAMPLE

Suppose you want to convert the fraction 2/3 into a percent.

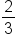
	Our Expression
	First, we will convert the fraction into a decimal using a calculator. 2 divided by 3 is equal to 0.6 repeating, or 0.6 with a bar above the 6. In order to round to the nearest percent, you want to use the 3 decimal digits, writing 0.6 repeating as 0.666
	Next, we want to convert the decimal to a percent form. To do this, multiply your decimal by 100 using your calculator. You can also do this without a calculator, as multiplying by 100 is the same as moving the decimal point two places to the right.
	Finally, we can round 66.6% to the nearest percent. Since the 6 after the decimal point is greater than 5, we can round up to 67%.

hint

Always make sure to include a percentage sign when writing numbers in percentage form.