Table of Contents |
A sampling distribution of sample means is a distribution that shows the means from all possible samples of a given size. Let’s start with an example of a sampling distribution.
Consider the spinner shown here:
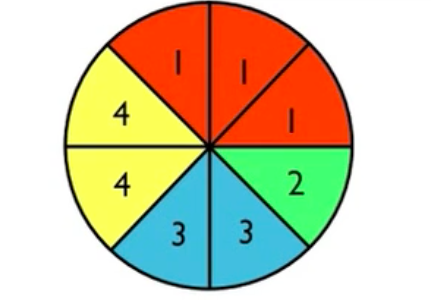
Suppose you spin it four times to obtain an average. You get a 2 the first time, a 4 the second time, a 3 the third time, and a 1 the fourth time. The mean is the average of 2, 4, 3, and 1 is:
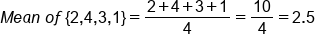
So, your first mean is 2.5.
| Sample | Mean |
|---|---|
| S1 = {2, 4, 3, 1} | x̄1 = 2.50 |
However, your mean won't be 2.5 every time. Suppose you repeat this process five more times to get the following six samples:
| Sample | Mean |
|---|---|
| S1 = {2, 4, 3, 1} | x̄1 = 2.50 |
| S2 = {1, 4, 3, 1} | x̄2 = 2.25 |
| S3 = {4, 2, 4, 4} | x̄3 = 3.5 |
| S4 = {2, 2, 3, 1} | x̄4 = 2.00 |
| S5 = {3, 1, 1, 1} | x̄5 = 1.50 |
| S6 = {1, 1, 1, 2} | x̄6 = 1.25 |
So how can we represent all these distributions?
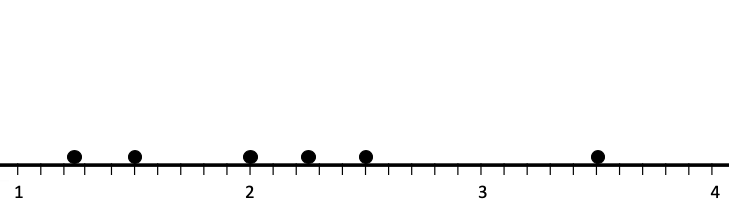
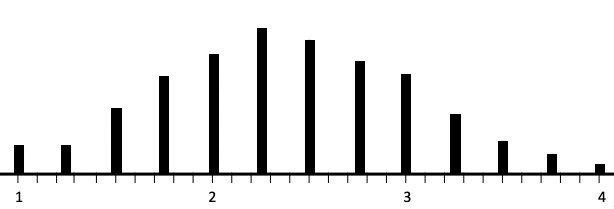
Source: THIS TUTORIAL WAS AUTHORED BY JONATHAN OSTERS FOR SOPHIA LEARNING. PLEASE SEE OUR TERMS OF USE.