Inverse Functions

1. Inverse Functions and Notation

In a function, the input variable undergoes one or more operations to yield a specific output value. We can think of this idea as x being the input to where the output value is y. We can say that

With inverse functions, the operations performed on the input variable are undone. This means that when y is put into the inverse function, the result will be the x value that produced y in the original function.

We can write this using inverse notation as: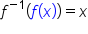

The above expression is telling us that if the value of a function, goes into an inverse function, the result will be the argument of the original function, x.

big idea

We use for inverse notation. Do not confuse the -1 with as an exponent.

2. Reverse Operations to Write Inverse Functions

We can write an inverse function by applying inverse operations in reverse order, according to operations that make up a function.

EXAMPLE

	Start with a number
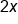
	Multiply it by 2
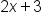
	Add 3 to it
	Our function

Let's work backward, and apply inverse operations from the steps above. This will lead to our inverse function:

	Start with a number
	Subtract 3
	Divide by 2
	Our inverse function

An inverse function undoes the operations performed on variables of a function. In the above example, x was multiplied by 2, and then 3 is added, we were able to write this as the function .

The steps to find the inverse to this function were to subtract 3 from the input value, and then divide by 2, so as to completely undo all operations of the original function. We write this as the inverse function .

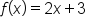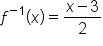Operations for function,	Operations for inverse function,
Start with x...	Starting with x...
1) Multiply by 2	1) Subtract 3
2) Add 3	2) Divide by 2
Our solution:	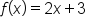Our solution:

3. The Graph of a Function and its Inverse

There is symmetry between the graph of a function and its inverse. The line acts as a line of reflection between a function and its inverse. This is characteristic of all functions and their inverses.

EXAMPLE

Below is the graph of and .



The line is a line of reflection between a function and its inverse. This means that if you have the graph of a function, you can grab the line , and use this line to plot points of the inverse function.

summary

In a function, an input value undergoes one or more operations, resulting in an output value. If the resulting output value is the argument of the functions inverse, it will return to the original input value. The function, describes a set of operations done to an input, x. The inverse function and notation is which describes the inverse operations of the original function We can write an inverse function by applying inverse operations in reverse order, according to operations that make up a function. For the graph of a function and its inverse, the line, y equals x is a line of symmetry of the function and its inverse.