Table of Contents |
As lines fit to data, figuring out the equations of those lines is the focus of this tutorial. You may recall the following linear equation:
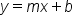
In the above equation, y and x are variables. Now, x is recognized as the explanatory variable and y as the response variable. The other two values are numbers, and they represent something.
The value of m is called the slope. The slope is a rate of change. You may have heard several terms of rates of change, like miles per hour or meters per second or miles per gallon in a car. In general, it's an increase of 1 in x corresponds to an increase or decrease of m in y.
EXAMPLE
If the rate of change was 30 miles per gallon, that means that an increase of one gallon would correspond to an increase of 30 miles that you could travel.The slope is calculated by taking the difference in y values divided by the difference in x values.

The other value, b, in the equation is called the y-intercept. It's the value of y when x is 0. So the line will pass through the point (0, b) on the y-axis.
Let's show these terms in practice, in the graph below.

To find the slope, what we have to do is find out the points that are on the line, and figure out by how much vertically this went up with an increase of 1 in x. Let consider how much it went up between 1 and 2 on the x-axis.

As the graph shows an increase of 1 in x, there was an increase of 2 in y. So the slope, which explains the rate of change that relates the increase in y to an increase of 1 in x, would be 2.
Also, the y-intercept is the point where the line passes through the y-axis, or at (0,1). So the value of y when x is 0 is 1, which would be b in the linear equation.

Below is the general linear equation compared to the formula used in statistics.

You may notice that the order is flipped, but it is still telling us the same information and can be used to find the best-fit line.
Suppose that you have a trend line and the equation is:


Suppose we don't know the equation of a trend line, but we know that it passes through (4, 500) and (12, 900).

To find the equation of that line, two pieces of information are needed: the slope and the y-intercept.
First, find the slope. You can see visually that from (4, 500) to (12, 900), it went up 8 in the x-direction. But it also actually went up 400 in the y-direction.

Recall that slope is the difference in y values divided by the difference in x values. So a change of 400 in the y-direction divided by a change of 8 in the x-direction means that for every 1 increase in the x-direction, it actually went up 400 divided by 8, or 50 in the y. Therefore, the slope, b1, is 50.



One thing that's important to note is that the best-fit line will change if you switch the explanatory and response variables. That's why it's important to choose at the beginning which one is the explanatory verses which one is the response variable.
EXAMPLE
Slope is a rate of change. So if you take a look below, miles per gallon would be the rate of change in the example on the right. If you switched to put gallons on the y-axis and miles on the x-axis, the rate of change here would actually be measuring gallons per mile, which is a different number.

|

|
One thing that's important to note, though, is that the value of the correlation coefficient is going to be the same for each of these two graphs, but the line itself is different, and that's why we need to choose which variable is the explanatory versus which one is the response.
Source: THIS TUTORIAL WAS AUTHORED BY JONATHAN OSTERS FOR SOPHIA LEARNING. PLEASE SEE OUR TERMS OF USE.