Table of Contents |
A literal equation is an equation that has more than one variable. In math, we work with literal equations all the time. For example, the slope–intercept form of a line is a literal equation: 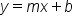 . This is because it has more than one variable.
. This is because it has more than one variable.
Formulas are common literal equations. Formulas relate variables together. For example, we can use a formula to relate the length and width of a rectangle to its area. We can rewrite formulas to create expressions for other variables in the equation.
EXAMPLE

|
Formula for the area of a rectangle |

|
Divide by w; expression for length |

|
Divide by l, expression for width |
We can rewrite literal equations to express other variables by applying inverse operations. More specifically, we look at what operations are being applied to the variable we wish to isolate, as well as in what order they are being applied. To isolate the variable, we apply the inverse operations in reverse order. This is shown below with several common formulas:
EXAMPLE
Use the formula for the area of a circle and solve for the radius, r.

|
Formula for the area of a circle |

|
Divide both sides by 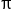
|

|
Take square root of both sides |
EXAMPLE
Use the formula for the distance and solve for rate, r.

|
Formula for distance, rate, and time |

|
Divide both sides by t |
EXAMPLE
Use the formula for the distance and solve for time, t.

|
Formula for distance, rate, and time |

|
Divide both sides by r |
EXAMPLE
Use the Pythagorean Theorem and solve for one side length,

|
Pythagorean Theorem |

|
Subtract  from both sides from both sides
|
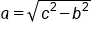
|
Take square root of both sides |
EXAMPLE
Use the Pythagorean Theorem and solve for the second side length, b.

|
Pythagorean Theorem |

|
Subtract  from both sides from both sides
|

|
Take square root of both sides |
Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License