 Specifically, this lesson will cover:
Specifically, this lesson will cover:
Table of Contents |
Factoring a quadratic is the opposite process of FOILing: we are taking a quadratic expression and rewriting it as two binomials being multiplied together. With basic factoring in the form  , we are seeking to identify two integers, p and q, such that:
, we are seeking to identify two integers, p and q, such that:
EXAMPLE
The quadratic expression factors to
factors to  , because
, because  , which is the constant term, and
, which is the constant term, and  , which is the coefficient of the x-term.
, which is the coefficient of the x-term.
Things get more complicated when the leading coefficient of the quadratic is other than 1, like 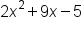 . This is because at least one of the binomials in factored form must have a coefficient of x other than 1, like
. This is because at least one of the binomials in factored form must have a coefficient of x other than 1, like  . If we start with FOIL, we can see this pattern:
. If we start with FOIL, we can see this pattern:

 (this is seen in the
(this is seen in the  term above) and also p by b (this is seen in the bpx term above).
term above) and also p by b (this is seen in the bpx term above).
Let's use this pattern to factor the following quadratic:
EXAMPLE
Factor .
.
 , so we can fill out part of it right now. Since 3 is a prime number, our only option for the factoring will be:
, so we can fill out part of it right now. Since 3 is a prime number, our only option for the factoring will be:

| p | q |
|---|---|
| 1 | -10 |
| 2 | -5 |
| -1 | 10 |
| -2 | 5 |
| p | + | 3q | = | p+3q |
| 1 | + | -30 | = | -29 |
| 2 | + | -15 | = | -13 |
| -1 | + | 30 | = | 29 |
| -2 | + | 15 | = | 13 |


|
FOIL the factored form by multiplying the first terms, 
|

|
Multiply the outside terms, 
|

|
Multiply the inside terms: 
|

|
Multiply the last terms: 
|

|
Combine like terms |

|
Our solution |
Another method for factoring quadratics with a leading coefficient other than 1 is to use the box method. In the box method, we'll be able to find the factored form,  and
and  , on the outside with the expanded form on the inside.
, on the outside with the expanded form on the inside.
Here is how to display the factors for the quadratic expression  using the box method.
using the box method.
|
|
2x | +3 |
|---|---|---|
|
x |

|
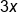
|
|
-4 |

|

|
Notice the inside of the box is an expanded form of  . The numbers
. The numbers  , 3x, -8x, and -12 can be combined to get the original expression of
, 3x, -8x, and -12 can be combined to get the original expression of  .
.
Also notice how we can multiply the factors at the top to get the answers inside the box, for example,  ,
,  ,
,  , and
, and  . With the box method, we'll fill out the inside of the box first and work our way backward to find the outside factors.
. With the box method, we'll fill out the inside of the box first and work our way backward to find the outside factors.
EXAMPLE
Factor .
.

|
|
|
|

|
| p | q |
|---|---|
| 1 | -30 |
| 2 | -15 |
| 3 | -10 |
| 5 | -6 |
| -1 | 30 |
| -2 | 15 |
| -3 | 10 |
| -5 | 6 |
 does not equal
does not equal  . Instead, we use these two numbers as coefficients to x terms to be included in the 2x2 box, along with the x-squared term and the constant term.
. Instead, we use these two numbers as coefficients to x terms to be included in the 2x2 box, along with the x-squared term and the constant term.

|
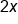 |
 |
 |
 is equal to
is equal to  , our original quadratic. If the sum doesn't add up, you've made an error somewhere.
, our original quadratic. If the sum doesn't add up, you've made an error somewhere.
 and -15x:
and -15x:
|
|
3x | |
|---|---|---|
|
|

|
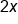
|
|
|

|

|
|
|
3x | +2 |
|---|---|---|
|
|

|

|
|
|

|

|
 and 2x:
and 2x:
|
|
3x | +2 |
|---|---|---|
|
x |

|

|
|
|

|

|
 out of
out of  and
and  :
:
|
|
3x | +2 |
|---|---|---|
|
x |

|
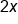
|
|
-5 |

|

|
|
|
3x | +2 |
|---|---|---|
|
x |

|
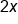
|
|
-5 |

|

|


Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License