Multiplying and Dividing Rational Expressions

1. Multiplying and Dividing Numeric Fractions

Before we discuss how to multiply and divide rational expressions (or algebraic fractions), it is helpful to review how we multiply and divide numeric fractions, because the process is the same, no matter what kind of fractions we are working with.

Multiplying two fractions is very straightforward. We simply multiply across the numerators and then multiply across the denominators. We should not forget to simplify the fraction if possible.

EXAMPLE

Multiply .

	Multiply the numerators and the denominators
	Evaluate the numerator and denominator
	Simplify
	Our solution

When dividing fractions, we actually write it as a multiplication problem, where we multiply the first fraction by the reciprocal of the second fraction. The reciprocal of a fraction is a fraction with the flipped quantities in the numerator and denominator.

EXAMPLE

Divide .

	Write as a multiplication problem using the reciprocal
	Multiply across numerators and denominators
	Simplify
	Our solution

2. Multiplying Rational Expressions

We multiply algebraic expressions in the same way that we multiply numeric fractions: we multiply across the numerators and multiply across the denominators. Once again, we make sure that our product is fully simplified by canceling out common factors that appear in both the numerator and denominator:

EXAMPLE

Multiply .

	Multiply across numerators and denominators
	Factor both and
	Cancel like terms in numerator and denominator
	Simplify
	Our solution

3. Dividing Rational Expressions

Dividing algebraic fractions works the same way it does when dividing numeric fractions. First, we write the problem as multiplication, using the reciprocal of the second fraction. Then we can follow the same procedure for multiplying rational expressions:

EXAMPLE

Divide .

	Write as multiplication, using reciprocal of second fraction
	Multiply across numerators and denominators
	Factor both and
	Cancel like terms in numerator and denominator
	Simplify
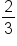
	Our solution