Table of Contents |
In review, the distributive property is used when simplifying an expression such as:

Using the distributive property, you would distribute the outside expression,  , to both terms inside the parentheses. Therefore, you would first multiply
, to both terms inside the parentheses. Therefore, you would first multiply  by the first term, noting that because both of the bases are x, you can add your exponents. Next, multiply
by the first term, noting that because both of the bases are x, you can add your exponents. Next, multiply  by your second term, -1. Thus, your final answer is:
by your second term, -1. Thus, your final answer is:

Your answer is in standard form, or descending order according to the exponents in each term.
Suppose you want to multiply two binomials:

To multiply binomials, you need to distribute twice, multiplying the 3x by both terms in the second parentheses, following by multiplying the 3 by both terms in the second parentheses. Note that 3x and 2x both have implied exponents of 1.

When distributing, you will write all terms as a single expression—adding terms with positive coefficients and subtracting terms with negative coefficients. Therefore, you can combine the like terms, -12x and 6x, which equals -6x, providing your final answer:

You can remember this method of multiplying binomials by using the acronym “FOIL,” which stands for “First, Outside, Inside, and Last.”

In the preceding example, you distributed by multiplying the first two terms in each parentheses and then the outside terms. You then distributed by multiplying the inside terms and then the last two terms in each parentheses. Therefore, you can use the acronym FOIL to remember the steps for distributing factors in binomial multiplication.

EXAMPLE
Use FOIL to multiply these two binomials:
 .
.


IN CONTEXT
Suppose a farmer wants to plant a small area for a new chicken pen. The length and width of the pen are shown below. What is the area of the chicken pen in terms of x?

To find the area of the pen, you want to multiply the length and the width, which would be expressed as:

These are binomials multiplied together, so you can multiply using FOIL:
- F Your first two terms, x and x, multiply together to give you x^2.
- O Your outside terms, x times 10, equal 10x.
- I Multiplying your inside terms, 3 and x, equals 3x.
- L Lastly, multiplying your last terms, 3 and 10, equals 30.

You can combine your like terms, 10x and 3x. Therefore, the area of the chicken pen can be written as:


Suppose you want to simplify:

This is an example of a binomial squared, and it means the same as:

You can multiply binomials squared in the same manner as other binomials, using FOIL: multiply your first two terms, your outside terms, your inside terms and finally, your last terms:

Combine your like terms, -5x and -5x, to provide your final expression:
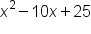
Source: This work is adapted from Sophia author Colleen Atakpu.