Odds are often confused with probability. However, odds are another way to express the likelihood that is different than probability. When you say that there is a 1 in 5 probability, that will be different than saying the odds in favor are 1 in 5.
IN CONTEXT
On this spinner, there are three 1's, a 2, two 3's, and two 4's.
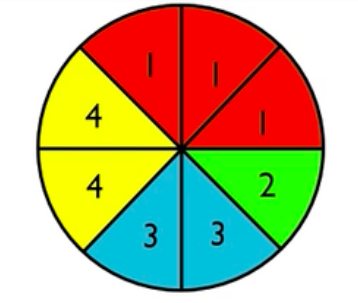
Suppose that 3 is a favorable outcome. Probability is the ratio of favorable outcomes to total outcomes. Since there are two 3's on the spinner, there are two favorable outcomes out of eight total outcomes. Therefore, 1/4 is the probability of 3.
Now we're going to contrast that with odds. The odds are the ratio of favorable outcomes to unfavorable outcomes. So, for a 3, there are two favorable outcomes, and there are six unfavorable outcomes. Therefore, the odds in favor of a 3 on the spinner are two to six, which can be reduced to one to three.
Odds in favor of 3 = 1:3
This says the odds in favor of a 3 are one to three, which means that for every one favorable outcome, there are three unfavorable outcomes.
Odds against are the ratio of unfavorable outcomes to the favorable outcomes, which means that there are three unfavorable to every one favorable. Odds against a 3 are three to one. Odds can also be expressed against an event simply by reversing the numbers you got when calculating the odds in favor of the event.
Odds against 3 = 3:1
Odds are usually expressed with a colon, rather than a fraction bar, although both are accepted. You should always reduce as if it was a fraction--in this case, for example, 6:2 reduced to 3:1, or 2:6 reduced to 1:3.
Let's convert probability to odds by exploring a few scenarios.
| Probability | Odds in Favor | Odds Against | Explanation |
|---|---|---|---|
P(heads on a coin) = 
|
1:1 | 1:1 | On a coin, there's one favorable and one unfavorable outcome. |
P(red in roulette) =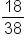 
|
18:20 = 9:10 |
20:18 = 10:9 |
On a roulette wheel, there are 18 favorable outcomes to 20 unfavorable outcomes, however, you must remember to reduce. This is also the same as 9 favorable outcomes to 10 unfavorable outcomes. |
P(4 on a fair die) =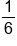 
|
1:5 | 5:1 | On the die, there is one favorable outcome and five unfavorable outcomes. |
Let's try another one.
| Probability | Odds in Favor | Odds Against | Explanation |
|---|---|---|---|
P(red) = 
|
7:11 | 11:7 | Of the 18 marbles, 7 of the marbles are red, and 11 of them are not red. |
P(green) =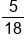 
|
5:13 | 13:5 | Of the 18 marbles, 5 of the marbles are green, and 13 of them are not green. |
P(blue) =  =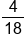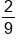 
|
4:14 = 2:7 | 14:4 = 7:2 | Of the 18 marbles, 4 of the marbles are blue, and 14 of them are not blue. This can be reduced: for every 9 marbles, 2 are blue and 7 are not blue. |
P(orange) =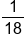 
|
1:17 | 17:1 | Of the 18 marbles, 1 of the marbles is orange, and 17 of them are not orange. |
Source: Adapted from Sophia tutorial by Jonathan Osters.
