Order of Operations: Exponents and Radicals

1. Exponents and Radicals

The order of operations outlines an order we should follow to evaluate expressions with multiple operations. We often use PEMDAS to remember the order of operations:

The "exponents" part of PEMDAS also includes radicals. We don't typically include "radicals" in the acronym, because all radicals can be written as exponents (fractional exponents, specifically). So as long as we remember that exponents and radicals are related, we can remember to evaluate both exponents and radicals after parentheses, but before multiplication, division, addition, and subtraction.

Let's focus first on evaluating expressions containing exponents:

EXAMPLE

	Evaluate
	Evaluate
	Add 8 to 16
	Our Solution

EXAMPLE

	Evaluate first
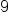	Multiply by
	Subtract 18 from 25
	Our Solution

When we encounter radicals (roots, such as square roots or cube roots), we treat them as being on the same level as exponents in the order of operations, and evaluate them before multiplication, division, addition and subtraction. This is illustrated in the examples below:

EXAMPLE

	Evaluate the square root first
	Multiply by
	Add 15 and 8
	Our Solution

EXAMPLE

	Evaluate the square root first
	Multipl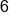y by
	Divide 30 by 2
	Our Solution

What do we do when an expression contains both exponents and radicals? Because exponents and radicals are at the same level according to the order of operations, we can think of their relationship as similar to multiplication and division, or addition and subtraction: we evaluate exponents and radicals as we see them reading left to right.

EXAMPLE

	Evaluate the square root first
	Evaluate the exponent
	Multiply by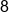
	Add 5 and 56
	Our Solution

term to know

PEMDAS

An acronym to remember the order of operations: parentheses, exponents, multiplication and division, addition and subtraction.