Outliers and Modified Boxplots

---

1. Outliers

You may recall that outliers are values that are far outside the pattern established by the rest of the data. They're either very high or very low in comparison to the rest of the data set.

Boxplots, introduced in another tutorial, are a way to graphically display the five number summary for a data set. This tutorial will present a modified version of boxplots so that it is easier to observe outliers in them.

EXAMPLE

Here is a set of test scores.

90, 98, 89, 88, 46, 90, 91, 84, 94

Almost everyone scored in the 80's or 90's, except for one student, who scored a 46. That student is an outlier.

terms to know

Outlier

A point that is so large or small as to be unusual, given the rest of the data points.

Modified Boxplot

A graphical display showing a modified version of the five number summary. If a distribution has outliers, then the "whiskers" only extend to the highest and lowest points that are not outliers.

---

2. The 1.5xIQR Rule

To make it easier to find outliers, there is a mathematical rule for determining whether a point is an outlier or not. This is called the “1.5xIQR rule.” IQR stands for Interquartile Range.

So, how do you use the 1.5xIQR method?

step by step

Step 1: Find the quartiles of the data set.
Step 2: Find the interquartile range (IQR).
Step 3: If we have a point that is 1.5 IQR's below the first quartile or 1.5 IQR's or more above the third quartile, then it is an outlier.

EXAMPLE

Consider the data set of test scores from above.

90

98

89

88

46

90

91

84

94

Step 1: First, find the quartiles of the data set. To do this, order the data from least to greatest. find the median, and find the medians within each of the low and high data sets.

46		84		88		89		90		90		91		94		98
		↑ Q1=86					↑ Median					↑ Q3=92.5

The median of this data set is 90. The median of the first quartile is actually between 84 and 88, or at 86, and the median of the third quartile is between 91 and 94, which is at 92.5.

Step 2: Next, find the interquartile range, or IQR. The interquartile range is the distance between the first and third quartiles. The difference between 92.5 and 86 is 6.5.

Step 3: Any point that is 1.5 IQR's below the first quartile or 1.5 IQR's or more above the third quartile will be considered an outlier.

1.5 IQR below the first quartile:

1.5 IQR above the third quartile:

This indicates that any test score higher than 102.25 points would be considered an outlier on the high side. Anything below 76.25 will be considered an outlier on the low side.

Of the test scores, only 46 falls outside this range, so this test score would be an outlier.

try it

Suppose that you have the data set of all house prices for homes purchased in Albuquerque, New Mexico, from February to April in 1993. These are in thousands of dollars.

The first and third quartiles have been calculated:

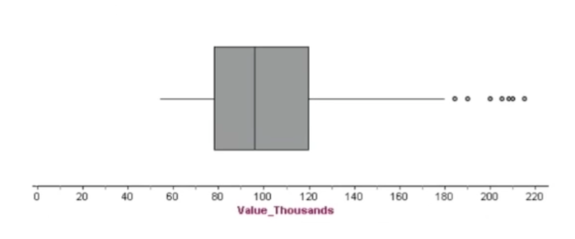
Home Prices in Albuquerque, New Mexico From February - April, 1993
205	72	93.9	99.5	87.5	105
208	72	82	97.5	88.9	104.5
215	74.9	78	97.5	85.5	105
215	73.1	77	90	83.5	102
199.9	72.5	70	96	81	100
190	67	62	86	80.5	103
180	215	54	169.5	79.9	97.5
156	159.9	107	155.3	75	95
145	135	210	125	75.9	94
144.9	129.9	72.5	130	75.5	92
137.5	125	66	102	75	94.5
127	123.9	60	102	73	87.4
125	120	58	92.2	72.9	87.2
123.5	112.5	184.4	92.5	71	87
117	110	158	89.9	77.3	86.9
118	108	69.9	85	69	76.6
115.5	105	133	87.6	67	73.9
111	104.9	116	89	61.9
113.9	95.5	110.9	87	129.5
99.5	93.4	112.9	70	97.5
Q1 = 78, Q3 = 120

What is the range for outliers? What is the lower fence for outliers and the upper fence for outliers?

IQR

1.5 IQR below the first quartile:

1.5 IQR above the third quartile:

The interquartile range is 42, so any point below 78 minus 1.5xIQR, which is 15, or above 120 plus 1.5xIQR, which is 183, will be an outlier.

Notice that there's nothing in the list below 15, but there are seven above 183. This means that there are seven outliers in this data set, which, by the way, is a completely legitimate and legal occurrence in this situation.

term to know

1.5xIQR Rule

If a point is larger than Q3 + 1.5xIQR, or smaller than Q1 - 1.5xIQR, then it is an outlier.

---

3. Boxplots

You can use this new information to create a new version of an already existing plot that you have. You’ve made boxplots in another tutorial; now you can modify them to show outliers.

Generally, you would make the whiskers on the box-and-whisker plot extend all the way out to the maximum and minimum. If the minimum or maximum (or both) are outliers, that will make the whiskers really long. For a modified boxplot, instead of going all the way out to those outliers, you can extend them only to the highest and lowest values that aren't outliers and notate the outliers separately.

EXAMPLE

Refer back to the student data set from the section above. Here are the values from least to greatest.

46		84		88		89		90		90		91		94		98
		↑ Q1=86										↑ Q3=92.5

Mark the same values that you would have if you were making a regular box-and-whisker plot. However, don’t go all the way down to 46 for your minimum--even though 46 is the actual minimum. 46 is an outlier, so instead go to the next lowest number that isn't an outlier---84--and make your line there. Then you can make your box and whiskers.

You still have to show the 46 as part of this data set somehow, so you will mark it with a dot. This is a modified boxplot.

In the home value data set, there were seven high outliers. This is a modified plot for that data set:

---