Output Optimization: Marginal Revenue / Marginal Cost

1. Marginal Revenue

We know that the point of owning a business is to make a profit, and profit equals revenues minus costs.

Profit = Revenues - Costs

In many tutorials, we will focus on revenue or cost, but in this tutorial, we will focus on both--putting it all together to determine where we can maximize profit.

Marginal revenue is the additional revenue we gain when we sell one more unit. It represents the change in total revenue (∆TR).

Here is an example of a perfect competitor--a price-taker--who sells their product for only one price, $20.

Quantity of T-Shirts	Total Revenue	Marginal Revenue
0	$0	--
1	$20	$20
2	$40	$20
3	$60	$20
4	$80	$20
5	$100	$20
6	$120	$20
7	$140	$20
8	$160	$20
9	$180	$20
10	$200	$20

When calculating marginal revenue for a perfect competitor, it is always going to be price, because the additional revenue gained each time you sell one more equals the only price that you can charge.

Therefore, marginal revenue and price are the same for our perfect competitor.

Here is their demand curve; it is a perfectly elastic demand curve, which shows that there is only one price.

That one price of $20 equals their marginal revenue, their demand curve, and price. Every time they sell one more, they gain the price of the product in additional revenue.

It also is the slope of total revenue because it measures the change in total revenue.

hint

Remember, slope is simply rise over run. It is the change in y as a proportion to the change in the x-axis, so it represents the change in total revenue.

Its slope is constant. The change in total revenue is the same every time--an additional $20.

This is why marginal revenue and demand in price is a horizontal line in a perfect competitor situation.

2. Marginal Cost

Marginal cost is the additional cost of producing one more unit (∆TC) and it is the change in total cost.

This scenario is a bit more complicated; it is not constant every time. We can see marginal cost initially falling, but then rising, so we are really looking at the change in total cost each time.

Quantity of T-Shirts	Total Cost	Marginal Cost
0	$30	--
1	$35	$5
2	$38	$3
3	$43	$5
4	$50	$7
5	$60	$10
6	$72	$12
7	$87	$15
8	$107	$20
9	$130	$23
10	$155	$25

If we graph these numbers, it looks like this blue line, which is the marginal cost curve.

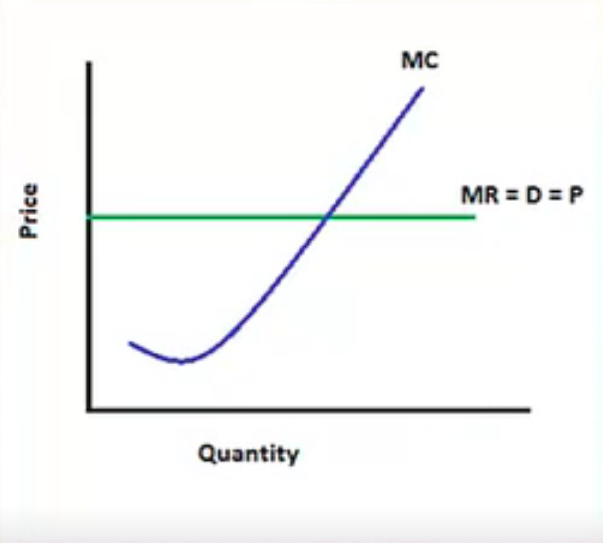
Just like marginal revenue was the slope of total revenue, this is the slope of total cost because it measures the change in total cost.

3. Maximizing Profit

Now, many people are under the impression that maximizing profit is about either minimizing cost or maximizing revenue.

However, this is not the case, as you can see in the chart below.

If we were minimizing costs, that would mean we would be producing nothing and profit is negative, because there is always a fixed cost that must be paid regardless of production levels.

Maximizing revenue is not the right course of action, either. Many people think that a firm should keep producing in order to make more profit, but as you can see, at some point profit begins to taper.

Instead, profit is the highest where there is the greatest difference between total revenue and total cost.

Note, it is also where marginal revenue and marginal cost are equal.

Why would we want marginal revenue and marginal cost to be equal? Why is that going to give us the highest profit?

Well, if marginal revenue is greater than marginal cost, that means that producing one more is going to add more to the revenue side of things than to the cost side of things--and increase profit.

EXAMPLE

For example, suppose we are selling six t-shirts and marginal revenue is $20, while marginal cost is $12. This means that the sixth t-shirt added $8 to profit, because $8 more went to revenue than to cost.

Therefore, you want to continue producing as long as marginal revenue is above marginal cost.

Conversely, if you look where marginal cost has jumped up above marginal revenue, now this is adding more to cost than to revenue.

EXAMPLE

If this firm were to produce the ninth t-shirt, they would add three more dollars to cost then they did to revenue, so profit would fall by $3, from $53 down to $50.

Therefore, they would want to scale back on production.

If we produce up to the point where marginal cost and marginal revenue are equal, this is where we will maximize profit.

hint

Now, these two are not always going to be equal. However, the idea is that you would never go past this point. You would want to stop before marginal cost jumped up above marginal revenue.

big idea

A firm should go up to the point where marginal revenue (MR) equals marginal cost (MC) to maximize profit or minimize loss.

4. Profit Maximizing Output: Graph

Let's pull it all together on a graph.

In the graph below, you can see marginal cost (blue line) and marginal revenue (green line). Note that the price, at $20, equals marginal revenue.

We've added an average total cost curve in red.

The first step, when looking at a graph like this, is to find the point where MR (marginal revenue) equals MC (marginal cost).

Now we know that the quantity that will maximize profit or minimize loss would be 8.

Now we read everything along the vertical gray line extending from 8. Is that a profit or loss?

Well, we know what we are generating in revenue, which is $20 times 8. But what is this costing us?

On this graph, you can see that the average total cost is around $13 per unit.

5. Total Revenue, Total Cost, and Profit: Graph

Looking at this graphically, the green area represents total revenue.

Price (P) = $20
Quantity = 8
Total Revenue (TR) = P x Quantity
TR = $20 x 8
TR = $160

You can verify all of these numbers by referring back to the chart.

Our total cost, then, would be the red rectangle.

Average Total Cost (ATC) = $13.38 (Total cost divided by quantity)
Quantity = 8
Total Cost (TC) = ATC x Quantity
TC = $13.38 x 8 TC = $107

Now, if we take the green rectangle, which was total revenue, and subtract out the red rectangle, which is total cost, we are left with profit.

There are two ways to look at profit: total revenue minus total cost, or graphically, here, it is the difference between the price per unit minus the cost per unit, or average total cost, times the quantity.

Profit = (P - ATC) x Quantity
Profit = (420 - $13.38) x 8 = $53

As mentioned, you could calculate total revenue minus total cost--$160 minus $107--and you would get the same thing.

We want to maximize the size of this green rectangle, because it represents profit.

You will notice that every single time we equate marginal revenue with marginal cost, this is the biggest the rectangle can get. If we move to the left or to the right, it will get smaller.

Therefore, if we set marginal revenue equal to marginal cost, we will always have the largest profit.