Polynomials Divided by Monomials

1. Basic Factoring

If terms in an expression share a common factor, it can be factored out of the expression. It may be helpful to think of this process as being the opposite of distribution.

EXAMPLE

Factor .

	Rewrite each term with the common factor of 4
	Factor out the 4 in each term
	Our solution

EXAMPLE

Factor .

	Rewrite each term with the common factor of -6
	Factor out the -6 in each term
	Rewrite parentheses as subtraction
	Our solution

As seen in the second example, you can factor out positive or negative factors. However, be sure to check the signs between terms in parentheses to make sure you have correctly factored a common factor. For the second term, 42, since we factored out a -6, we would multiply -6 by -7 to represent the positive 42.

hint

You can test your factored answer by using distribution to expand the expression.

EXAMPLE

Distribute .

	Distribute -6 into each term in the parentheses
	Evaluate multiplication
	Evaluate

2. Factoring out an Algebraic Factor

We can use this factoring technique to factor out more than just numbers. If algebraic expressions share variable factors, we can factor them out as well.

EXAMPLE

Factor .

	Rewrite each term with factors
	Factor out the common factor of 2x from each term
	Factoring out 2x

hint

It helps to break down coefficients into prime factors. Doing so in the example above makes it clearer to see how 2x is a common factor. Additionally, if an entire term is the factor being factored out, what remains is 1. This is why the binomial in parentheses above is .

3. Dividing a Polynomial by a Monomial

Sometimes when dividing a polynomial by a monomial, there are common factors between the monomial term and terms that make up the polynomial. In this case, it is relatively straightforward to divide coefficients and decrease exponents.

EXAMPLE

Divide by .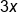

	Rewrite each term with a common factor of 3x
	Rewrite as separate fractions
	Divide each term in the numerator by the denominator
	Our solution

Of course, such examples that divide nicely between all terms are not always the case when dividing polynomials. When we need to divide a term that doesn't share all common factors, we divide what we can, and express the remainder as a fraction.

To show this, let's look at a different example where the first couple of terms divide evenly, but the last term does not. Take note of how we write the division:

EXAMPLE

Divide by .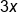

	Rewrite as separate fractions
	Rewrite each expression with common factors
	Divide the numerator by the denominator in each term using common factors
	Our solution

We were able to factor out 3x from , , and . However, the only common factor between 6 and 3x is the 3, not the x. So this term becomes a fraction, and due to the common factor of 3, we were able to simplify it to 2 divided by x.