Positive and Negative Correlations

1. Correlations

Correlation is going to allow you to observe the strength and direction of a linear association between two quantitative variables. Recall that it is a number between negative 1 and positive 1.

• Any correlation coefficient between negative 0.5 and positive 0.5 is considered a weak association between the two quantitative variables.
• Any correlation coefficient between positive 0.5 and positive 0.8, or negative 0.5 to negative 0.8, is considered a moderately strong correlation.
• Any correlation coefficient between positive 0.8 to positive 1, or negative 0.8 to negative 1 is considered a very strong correlation.

1a. Positive and Negative Correlation

A positive correlation is going to be a tendency of the response variable to increase in response to an increase in the explanatory variable.

EXAMPLE

Below is a visual representation with a correlation coefficient, r, of positive 0.7. Even though the direction is positive, the association is not terribly strong.


r = 0.7

EXAMPLE

Below is a visual representation with a correlation coefficient, r, of negative 0.99. This means it's almost a perfectly straight linear relationship. It is a negative correlation because as the explanatory variable on the x-axis increases, the response variable on the y-axis has a tendency to decrease.

r = -0.99

terms to know

Positive Correlation

The type of correlation present when two variables have a correlation coefficient generally greater than or equal to 0.5.

Negative Correlation

The type of correlation present when two variables have a correlation coefficient generally less than or equal to -0.5.

1b. Relative Zero Correlation

Some graphs will appear to be a cloud. In this case, the relationship will have a relative zero correlation. There's no discernible association between the explanatory and the response.

EXAMPLE

Below is a visual representation with a correlation coefficient, r, of zero.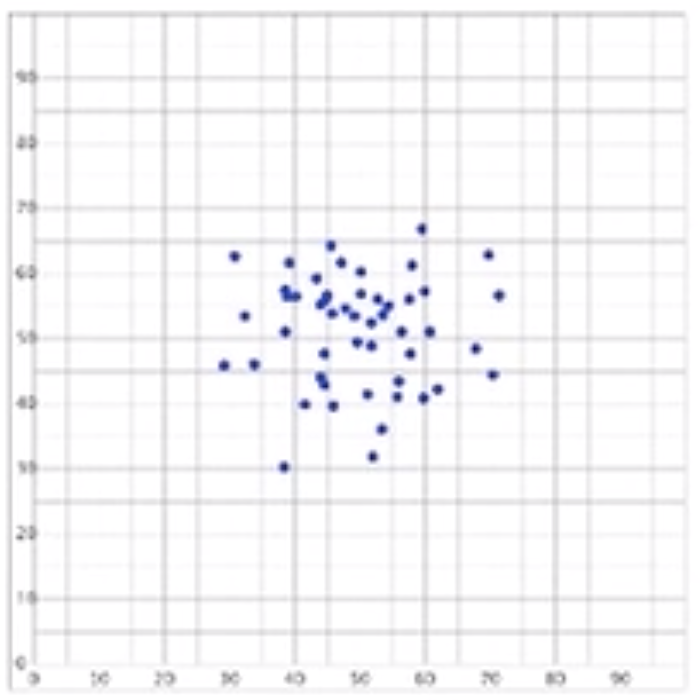

r = 0

hint

If all the points lined up in a straight horizontal line, that would also give you a correlation coefficient of zero.

term to know

Relative Zero Correlation

The type of correlation present when two variables have a correlation coefficient generally between -0.5 and 0.5.

1c. Non-Linear Relationship

One thing that's worth noting is that the numbers, like correlation, very rarely tell the entire story.

EXAMPLE

Consider the two tables below.

Table 1			Table 2
x	y		x	y
10	804		10	914
8	695		8	814
13	758		13	874
9	881		9	877
11	833		11	926
14	996		14	810
6	724		6	613
4	426		4	310
12	1,084		12	913
7	482		7	726
5	568		5	474
r = 0.82			r = 0.82

If you take a look at these two tables, the correlation coefficient for each of them is 0.82 in both cases. Based on that, you might think that they look similar when they are graphed. However, this is not the case.

With the first graph, you can see it's a fairly strong positive association, just as you would expect.

With the second graph, it's a strong association, but it's not linear. This follows the form for a non-linear relationship. If x and y have a nonlinear relationship, a line isn't going to model this accurately at all. Even though they have the same correlation coefficient, one has a line being a correct model for the data set, and the other does not.

If you see that the correlation is a number that is very, very low--near zero--you might assume there's no relationship between x and y. However, you could be wrong.

EXAMPLE

Consider this data set.

x	y
1.2	23.3
2.5	21.5
6.5	12.2
13.1	3.9
24.2	4
34.1	18
20.8	1.7
37.5	26.1
r = 0.00099

The correlation coefficient for this data is very low. You may assume that there is no relationship. Let's see what the graph of this data looks like.



You can see there's a clear trend in the data set; however, it is non-linear.

big idea

It is important to know that the correlation coefficient, r, only measures the strength of a linear relationship between x and y. To really understand a relationship between two variables, it is crucial to always graph your data.

term to know

Non-Linear Relationships

Associations between two variables that can be modeled better with a curve than a line.